Момент силы относительно точки и оси

Плечо силы

Кратчайшее расстояние от оси вращения до точки приложения силы называется плечом силы. Это длина перпендикуляра, опущенного из центра вращения на линию действия силы: Линия действия силы - линия, вдоль которой направлен вектор силы. $$ M = F·l = F·r·sin(\alpha) $$ или $$ \vec{M} = \vec{F}\cdot \vec{r} $$ Размерность: [M]= Ньютон · метр,
F — Приложенная сила (Ньютон),
r — расстояние от центра вращения до места приложения силы (метр),
l — длина перпендикуляра, опущенного из центра вращения на линию действия силы (метр),
α — угол, между вектором силы F и вектором положения r

Чтобы найти плечо силы, надо взять линейку и, совместив ее с направлением силы, провести линию. Взять угольник с прямым углом и провести из точки вращения на эту линию перпендикуляр. Взять линейку и измерить длину этого перпендикуляра. ЭТО И БУДЕТ ПЛЕЧО СИЛЫ

Что называется моментом силы?

Момент силы (синонимы: крутящий момент, вращательный момент, вертящий момент, вращающий момент) — векторная физическая величина, равная векторному произведению радиус-вектора (проведённого от оси вращения к точке приложения силы — по определению), на вектор этой силы. Характеризует вращательное действие силы на твёрдое тело.

Моментом силы называют произведение силы на плечо: \( M = F d;\;\;\;F - \text{сила;}\;\;\;d - \text{плечо}.\)

Единица измерения момента силы: 1 Ньютон умножить на метр.

Момент силы применяется ко всем вращающимся телам, каковым, в частности, является рычаг. Момент силы получается, если саму силу умножить на плечо силы.
Эта величина полезна в решении задач, когда на рычаг действует не две силы, а больше: три, четыре и т.д. При этом некоторые из этих сил вращают рычаг по часовой стрелке, а некоторые – против. Вот тут без учёта моментов не обойтись.

По какой формуле рассчитывается момент силы?

Если:
M — момент силы (Ньютон · метр),
F — Приложенная сила (Ньютон),
r — расстояние от центра вращения до места приложения силы (метр),
l — длина перпендикуляра, опущенного из центра вращения на линию действия силы (метр),
α — угол, между вектором силы F и вектором положения r (сила действует под углом), 
то: $$ M = F\cdot l = F\cdot r\cdot sin(\alpha)$$ или в виде векторного произведения: $$ \vec{M} = \vec{F}\cdot \vec{r} $$

Момент силы относительно точки

Если имеется материальная точка Of, к которой приложена сила F, то момент силы \(\vec{M_o}\) относительно точки O равен векторному произведению радиус-вектора \(\vec{r}\), соединяющего точки O и Of, на вектор силы \(\vec{F}\).

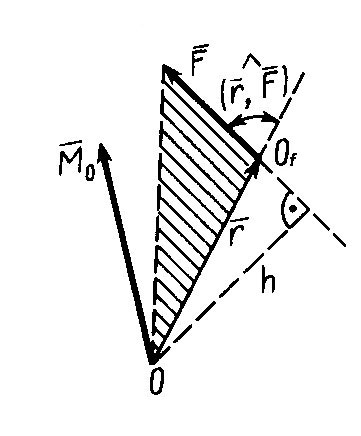
Чтобы найти момент силы относительно точки, нужно:

• продлить мысленно линию действия силы вперед, или назад (по обстоятельствам),
• из точки вращения опустить перпендикуляр на линию действия силы, и найти его длину (вот тут как раз может пригодиться синус угла)
• умножить силу на длину перпендикуляра в одной системе единиц. Получим величину момента силы.

Следует помнить, что это вектор, и он всегда перпендикулярен плоскости вращения, то есть плоскости, проходящей через точку вращения и линию действия силы. И направлен в ту сторону от плоскости, чтобы вращение под действием силы вокруг точки было видно с его конца против часовой стрелки.

Момент кручения направлен таким образом, что если смотреть с конца его вектора на вращающийся рычаг, то последний будет двигаться против хода стрелки часов. Общепринято считать это направление момента положительным при решении разного рода задач.

Момент силы относительно оси

Моментом силы относительно оси называется алгебраический момент проекции этой силы на плоскость, перпендикулярную оси, относительно точки пересечения оси с этой плоскостью: $$ M = \pm \vec{F’}·h $$

Таким образом, момент силы есть величина векторная. И вектор момента силы направлен так, чтобы из его конца вращение от а к b происходило против часовой стрелки.

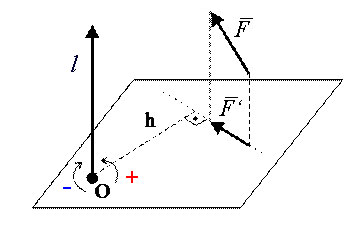
Как определяется величина и направление вектора момента силы?

Момент силы — аксиальный вектор. Он направлен вдоль оси вращения.
Направление вектора момента силы определяется правилом буравчика или правилом правой руки, а величина его равна M.

Правило правой руки можно сформулировать таким образом: если согнуть в полудугу четыре пальца правой руки и направить эту полудугу так, чтобы она шла вдоль первого вектора (первый множитель в формуле) и направлялась к концу второго, тогда оттопыренный вверх большой палец укажет направление момента кручения. Отметим также, что перед тем как использовать это правило, необходимо установить умножаемые вектора так, чтобы они выходили из одной точки (их начала должны совпадать).