Понятие силы натяжения нити
Сила натяжения нити является реакцией подвеса (нити), на действие со стороны тела на подвес. Сила натяжения нити всегда имеет направление вдоль нити.
Если следует учитывать растяжение нити, при этом нагрузки малы, а нить упругая, то при вычислении силы натяжения используют закон Гука: $$ \vec{N}=\vec{F_u}=k\Delta\vec{l} $$ где \(F_u\) - сила упругости нити; k - коэффициент упругости нити; \(\Delta l\) - удлинение нити.
Единицей измерения силы натяжения нити в Международной системе единиц (СИ) (как и для любой другой силы) является ньютон
Свойства нити в задачах школьного курса физики
Нить, обычно, не имеет массы (невесомая), не трётся (скользит без трения), гнется под любым углом без усилия (абсолютно гибкая), натяжение в нити всегда направлено вдоль нити, причем натяжение везде вдоль нити одинаковое и неотрицательное (т.е. - может быть только растяжение, сжатия не бывает), нить не растягивается (нерастяжимая).
Если нить невесома и нерастяжима, то такую нить рассматривают как проводник силы.
В зависимости от условий сила натяжения нити рассчитывается по-разному:
Нить с неподвижно закрепленным верхним концом
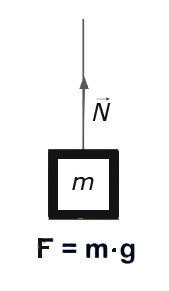
Простейшим примером проявления силы натяжения является нить с закрепленным на ней грузом. Верхний конец такого подвеса фиксируется неподвижно. В этом случае сила натяжения будет соответствовать силе тяжести, которая действует на тело. Формула для расчета: $$ F=F_{тяж}=m\cdot g $$ где m – это масса тела, а g представляет собой ускорение свободного падения.
Нить расположена под углом (маятник)
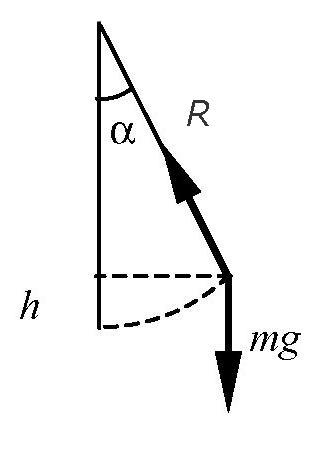
В случае, когда груз расположен под определенным углом, характер силы натяжения несколько изменяется. Примером такой системы выступает маятник. $$ F_n=m\cdot g\cdot cos(\alpha) $$ где α равен углу отклонения.
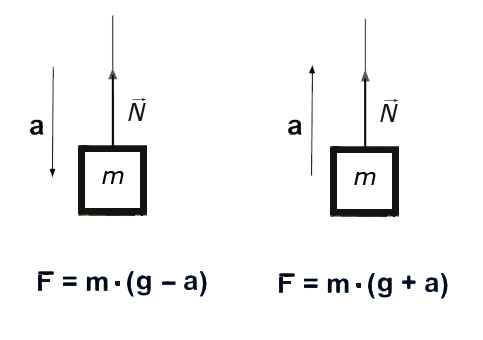
Груз движется вверх с ускорением
На груз действует сила натяжения, приводящая его в движение вверх с ускорением a. В этом случае следует использовать такую формулу: $$ F=F_{тяж} + m\cdot a $$
Груз вращается на нити
Один конец нити закреплен, другой вращается с закрепленным на конце грузом. Сила натяжения, возникающая внутри подвеса, характеризуется центробежной силой и в случае вращения в вертикальной плоскости циклически претерпевает изменения (ведь сила притяжения постоянно действует на объект и тянет его вниз). То есть можно наблюдать зависимость силы от угла отклонения от вертикали:
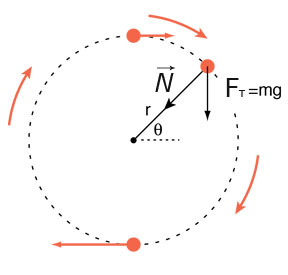
- приближение к земле приводит к увеличению силы;
- во время удаления от земли сила слабеет.
Чем быстрее движется объект, тем больше центробежная сила.
Формула расчета: $$ F=\frac{m\cdot ν^2}{r} $$ где v – скорость вращения подвешенного груза, а r – радиус окружности, по которому вращается груз.Груз тянут за нить, преодолевая силу трения
Случай, когда присутствует сила трения, которая способствует увеличению силы натяжения (груз тянут за нить). Общее натяжение в данном случае вычисляется по формуле: $$ F_н = F_{тр} + F_у $$
где \(F_{тр}\) – трение, а \(F_у\) – ускорение.
$$ F_{тр} = mkP $$где mk – трение между объектами, а P – сила взаимодействия между ними.
При расчетах нужно помнить, что трение покоя — это трение, которое возникает в результате попытки привести объект, находящийся в покое, в движение — отличается от трения движения — трения, возникающего в результате попытки заставить движущийся объект продолжать движение.Сила натяжения нити, перекинутой через блок
Во многих задачах на натяжение нити фигурирует неподвижный блок. Блок — простой механизм, который состоит из подвесного диска. Это помогает ему изменять направление силы натяжения нити.
Во многих физических задачах блоки являются идеальными — не обладают массой, трением, не ломаются, не отделяются от нити, не деформируются.
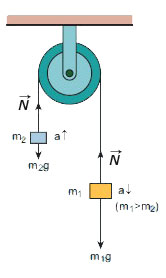Если участки нити, перекинутой через блок, параллельны (грузы подвешены вертикально), то натяжение на всех участках становятся одинаковым, даже если оба конца натягиваются силами различных величин.
Для системы масс, подвешенных вертикально через блок, сила натяжения будет равна: $$ T=\frac{2g\cdot m_1\cdot m_2}{m_2+m_1} $$ В приведенной формуле g - ускорение свободного падения, m_1 — масса первого тела, m_2 — масса второго тела.
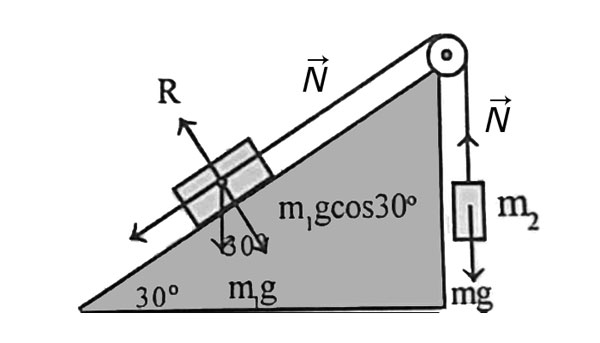
- Если участки нити, перекинутой через блок, не параллельны, то такую систему можно представить в виде треугольника с углами в точках с первых грузом, вторым и самим блоком. В этом случае натяжение в веревке зависит как от силы тяжести, так и от составляющей силы натяжения, которая параллельна к диагональной части веревки.
Если участки нити, перекинутой через блок, параллельны (грузы подвешены вертикально), то натяжение на всех участках становятся одинаковым, даже если оба конца натягиваются силами различных величин.
Может ли сила натяжения нити быть отрицательной? И сонаправлена ли она с ускорением?
Сила - не может, а проекция силы на ось - может быть отрицательной, в зависимости от взаимного направления вектора силы и направления оси. Если нить удерживает два тела разной массы через блок, то ускорение одного из них сонаправлено с силой натяжения нити а ускорение другого - противоположнонаправлено.
Как находится сила натяжения нити при колебаниях математического маятника?
Когда маятник висит по отвесу, сила тяжести уравновешивается силой натяжения нити При отклонении маятника из положения равновесия на некоторый угол φ появляется касательная составляющая силы тяжести Fτ = – mg sinφ. Знак "минус" в этой формуле означает, что касательная составляющая направлена в сторону, противоположную отклонению маятника.
Как вычислить силу натяжения нити отклоненного маятника?
Проще считать через энергию. Наверху, когда маятник отклонен в крайнее положение, у тела энергия потенциальная: $$ E = mg\cdot R(1-cos\alpha) $$ где R - длина нити, а в нижнем положении - кинетическая энергия E = mv²/2. Отсюда $$ v=\sqrt{2gR(1-cosα)} $$ Теперь найдем силу натяжения нити, расписав силы по осям. $$ T = mg + \frac{mv^2}{R} $$ (где T- сила натяжения нити, mv²/R-центробежная сила, а знак +, так как их векторы направлены в одну сторону)
Таким образом, сила натяжения нити отклоненного маятника: $$ T=mg+m2g(1-cos\alpha) = mg(3-2cos\alpha) $$
