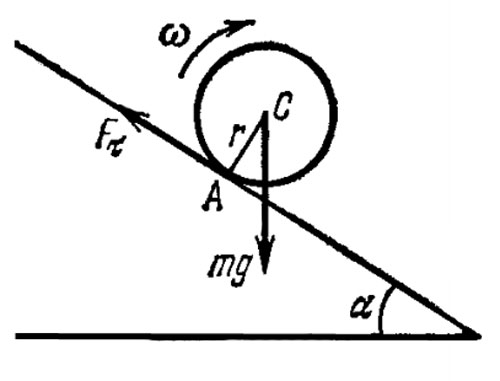
Пусть скатывающееся тело обладает симметрией вращения относительно геометрической оси С. Будем предполагать, что при движении не возникает скольжения. Это означает, что скорость тела в точке касания А равна нулю. Отсутствие скольжения обеспечивается действием сил со стороны наклонной плоскости на скатывающееся тело. Эти силы сводятся к силе нормального давления \(F_n\) и к касательной силе трения \(F_{\tau}\).
При отсутствии скольжения сила \(F_{\tau}\) - сила трения покоя или сила трения сцепления.
Величина силы \(F_{\tau}\) может принимать любое значение от 0 до \(kF_n\), где k — коэффициент трения. При качении она устанавливается как раз такой, чтобы не было скольжения. Если касательная сила, требующаяся для этого, превышает \(kF_n\), то чистое качение невозможно — оно будет сопровождаться скольжением.
Так как на скатывающееся тело действует сила трения, то может возникнуть вопрос, почему в рассматриваемой задаче можно применять закон сохранения энергии в его механической форме.
Ответ заключается в том, что при отсутствии скольжения сила трения приложена к тем точкам тела, которые лежат на мгновенной оси вращения. Мгновенная скорость таких точек равна нулю, а потому приложенная к ним сила трения сцепления работы не производит и не влияет на величину полной кинетической энергии скатывающегося тела.
Роль силы трения сцепления \(F_{\tau}\) сводится к тому, чтобы привести тело во вращение и обеспечить чистое качение. При наличии силы трения сцепления работа силы тяжести идет на увеличение кинетической энергии не только поступательного, но и вращательного движения тела.
Момент инерции относительно оси
Во вращательном движении в качестве меры инертности используется момент инерции (тело одной и той же массы при вращении относительно разных осей обладает разной инертностью, поэтому массой в качестве меры инертности вращающихся тел пользоваться нельзя).
Момент инерции тела относительно неподвижной оси z равен сумме произведений элементарных масс на квадрат расстояния от оси вращения до данной элементарной массы. $$ I_z = \sum_i\Delta m_ir_i^2 $$Момент инерции относительно неподвижной оси есть величина скалярная.
В СИ момент инерции измеряется в килограммах на метр в квадрате (кг-м2).
На практике вычисление момента инерции производится путём интегрирования: $$ I =\int r^2dm = \int\rho r^2dV $$ где dm - элементарная масса; dV - элементарный объём (объём, занимаемый элементарной массой); r - расстояние от элементарной массы до оси вращения; ρ - плотность тела в данной точке.
Вычисление этого интеграла в общем случае может быть довольно сложным, но если тело однородно, т.е. плотность тела во всех его точках одинакова, то плотность можно вынести за знак интеграла:
$$ I= \rho\int r^2dV $$В таблице приведены моменты инерции некоторых тел, встречающихся в задачах по данной теме:
| Тонкое кольцо |  |
\(mr^2\) |
| Полый тонкостенный цилиндр |  |
\(mr^2\) |
| Сплошной цилиндр |  |
\(\frac{m}{2}r^2\) |
| Полый толстостенный цилиндр |  |
\(\frac{m}{2}(r_1^2+r_2^2)\) |
| Диск |  |
\(\frac{m}{2}r^2\) |
| Диск |  |
\(\frac{m}{4}r^2\) |
| Шар |  |
\(\frac{2m}{5}r^2\) |
| Полая тонкостенная сфера |  |
\(\frac{2m}{3}r^2\) |
| Тонкий стержень длиной L |  |
\(\frac{m}{12}l^2\) |
| Прямоугольная пластина |  |
\(\frac{m}{12}l^2\) |
Решение задач "тело скатывается ..."
- Уравнение моментов относительно мгновенной оси вращения. При отсутствии скольжения мгновенная ось проходит через точку касания А. Так как мгновенная ось и ось, проходящая через центр масс С, движутся параллельно друг другу, то уравнение моментов имеет обычную простую форму:
$$ I_A \frac{\Delta \omega}{\Delta t} = М_A $$
где \(I_A\) — момент инерции скатывающегося тела относительно мгновенной оси, а \(M_A\) — момент внешних сил относительно той же оси. Внешними силами является сила тяжести mg и реакция опоры, действующая со стороны наклонной плоскости на скатывающееся тело. Сила реакции опоры выпадает из уравнения моментов, так как она проходит через ось A, и ее момент относительно этой оси равен нулю. Таким образом,
$$ I_A \frac{\Delta \omega}{\Delta t} = mgr sin\alpha $$
Обозначим v линейную скорость точки С. Она связана со скоростью \(v_A\) точки А тела соотношением
$$ v = v_A + \omega r $$
При отсутствии скольжения \(v_A\) = 0, а потому \(v = \omega r\).
Для линейного ускорения точки С получаем \(а = \frac{\Delta v}{\Delta t} = r\frac{\Delta\omega}{\Delta t}\). Поэтому предыдущее уравнение дает $$ a = \frac{mgr^2}{I_A}sin\alpha $$ По теореме Гюйгенса-Штейнера \(I_A = I_c + mr^2\), где \(I_c\) — момент инерции тела относительно оси, проходящей через центр масс С. Следовательно, $$ a=\frac{g sin\alpha}{1+\frac{I_c}{mr^2}} \;\;\;(1) $$ Преимущество данного способа в том, что в исходное уравнение не входит неизвестная реакция опоры.Теорема Гюйгенса-Штейнера гласит: момент инерции тела относительно произвольной оси равняется сумме момента инерции тела относительно оси, проходящей через центр масс параллельно произвольной оси и произведения массы тела на квадрат расстояния между осями $$ I=I_c + md^2 $$
- Уравнение моментов относительно оси, проходящей через центр масс С. Оно также имеет простой вид
$$ I_c \frac{\Delta \omega}{\Delta t} = М_c $$
где \(М_с\) — момент внешних сил относительно оси С. В это уравнение не войдет сила тяжести, так как она проходит через ось С. Момент создается силой реакции опоры. При этом играет роль только слагаемая \(F_{\tau}\) этой силы, параллельная наклонной плоскости, т. е. сила трения сцепления. Ее момент \(M_c = rF_{\tau}\), а потому
$$ I_c \frac{\Delta \omega}{\Delta t} = rF_{\tau} $$
Это уравнение содержит два неизвестных: угловое ускорение \(\frac{\Delta \omega}{\Delta t}\) и силу \(F_{\tau}\). Недостающее уравнение дает теорема о движении центра масс:
$$ m\frac{\Delta v}{\Delta t}= mg sin\alpha - F_{\tau} $$
Присоединив сюда прежнее соотношение \(а = \frac{\Delta v}{\Delta t} = r\frac{\Delta\omega}{\Delta t}\) и разрешив полученные уравнения относительно а, получим формулу (1), как в предыдущем случае.
Кроме того, получаем следующее выражение для силы трения сцепления: $$ F_{\tau}=\frac{I_c}{I_c + mr^2}mg sin\alpha $$ - Закон сохранения энергии. Кинетическая энергия тела равна
$$ K = \frac{1}{2}I_A\omega^2 $$
Поэтому
$$ K = \frac{1}{2}I_A\omega^2 = mgh $$
где h — высота, с которой опустилось тело при скатывании из состояния покоя.
Если оно прошло вдоль наклонной плоскости путь x, то \( h = х sin\alpha\), и, следовательно, $$ \frac{1}{2}I_A\omega^2 = \frac{I_A}{2r^2}v^2 = mgx sin\alpha $$ Дифференцируя это соотношение по времени и замечая, что \(\frac{\Delta x}{\Delta t}= v\), снова получим формулу $$ a = \frac{mgr^2}{I_A}sin\alpha $$
Радиус инерции, радиус качения тела
Радиусом инерции тела относительно оси называется линейная величина, геометрически равная расстоянию от оси z той точки, в которой надо сосредоточить массу всего тела M, чтобы момент инерции одной этой точки был равен моменту инерции всего тела. $$ I_z = M\rho_z^2 $$ где М — масса тела. Зная радиус инерции, можно по данной формуле найти момент инерции тела и наоборот.
Если радиус инерции ввести в формулу для ускорения (1), то она примет вид: $$ a=\frac{g sin\alpha}{1+(\frac{\rho}{r})^2} $$
Величину r можно назвать радиусом качения тела. Радиус качения есть расстояние между центром масс скатывающегося тела и мгновенной осью вращения. Для цилиндра или шара радиус качения равен геометрическому радиусу этих тел.
Ускорение скатывающегося тела и приобретенная им скорость поступательного движения зависят от отношения радиуса инерции к радиусу качения. Чем больше это отношение, тем медленнее скатывается тело.
Легче всего это понять с помощью закона сохранения энергии.
Если тело скатывается с высоты h, то вся его потенциальная энергия mgh переходит в кинетическую. Последняя складывается из кинетических энергий поступательного и вращательного движений. Полная кинетическая энергия тела в нижнем положении равна mgh, т. е. зависит только от высоты h. Чем большая доля кинетической энергии приходится на вращение тела, тем медленнее оно скатывается с наклонной плоскости. Отношение кинетической энергии вращательного движения к кинетической энергии поступательного движения равно:
$$ \frac{E_{вр}}{E_{пост}} = \frac{I_c\omega^2}{mv^2} = (\frac{\rho}{r})^2 $$
Максимальное значение для ускорения а получается в случае чистого скольжения при отсутствии сил трения.
Полые тела скатываются медленнее, чем сплошные тела той же геометрической формы.
При одинаковых массах моменты инерции полых тел больше, чем сплошных. Поэтому на долю вращательного движения у полых тел приходится относительно большая кинетическая энергия, чем у сплошных.
Когда угол наклона а равен нулю, ускорение а обращается в нуль. Вместе с ним обращается в нуль и сила трения сцепления \(F_{\tau}\). Таким образом, твердое тело, обладающее осевой симметрией, например цилиндр или шар, при отсутствии скольжения катится по твердой горизонтальной плоскости прямолинейно и равномерно, совсем не испытывая силы сопротивления. Этот результат относится к идеализированным моделям тел. Тело и плоскость, по которой оно катится, должны быть идеально твердыми и гладкими.
В реальных условиях тело и плоскость деформируются. На плоскости возникает углубление, тело соприкасается с ней не в одной геометрической точке, а на некотором участке конечной площади. В результате при качении по горизонтальной плоскости возникает сила, замедляющая движение - сила трения качения. Она обычно мала по сравнению с силой трения скольжения, и во многих случаях ею можно пренебречь.