Тело на наклонной плоскости

Что такое наклонная плоскость?

Наклонная плоскость - это плоская поверхность, установленная под углом к горизонтали. Наклонная плоскость является одним из простых механизмов. Она позволяет поднимать груз вверх, прикладывая к нему усилие, заметно меньшее, чем сила тяжести, действующая на этот груз.

Наклонная плоскость подчиняется "золотому правилу механики". Чем меньше угол между поверхностью и наклонной плоскостью (т.е. чем она более пологая, не круто поднимающаяся вверх), тем меньше надо прикладывать сил для подъема груза, но и большее расстояние необходимо будет преодолеть.

Где и как используется наклонная плоскость? Разновидности

Наклонная плоскость применяется для того, чтобы тело большей массы можно было перемещать действием силы, значительно меньшей веса тела.

Клин - одна из разновидностей простого механизма под названием "наклонная плоскость". Клин состоит из двух наклонных плоскостей, основания которых соприкасаются, и изменяет направления действия силы.

Чтобы расколоть полено, в трещину на его торце вставляют металлический клин и бьют по нему обухом топора или молотком. Сила, с которой клин раздвигает половинки бревна, гораздо больше силы, с которой молот воздействует на клин. Выигрыш в силе в данном примере равен отношению длины клина к толщине на тупом конце.

Винт - наклонная плоскость, навитая на ось. Резьба винта – это наклонная плоскость, многократно обернутая вокруг цилиндра. В зависимости от направления подъема наклонной плоскости винтовая резьба может быть левой или правой.

Примеры простых устройств с винтовой резьбой – домкрат, болт с гайкой, микрометр, тиски.

Наклонная плоскость в быту

Пандусы для подъема вверх, конвейеры; зубило для разрубания металла, топор для рубки, ножи и мечи, наконечники копий и стрел, ножницы, мясорубка.

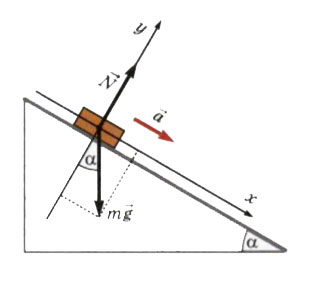
Соскальзывание тела с наклонной плоскости

$$ mg_y = -mg cos\alpha \\ mg_x = mg sin\alpha $$

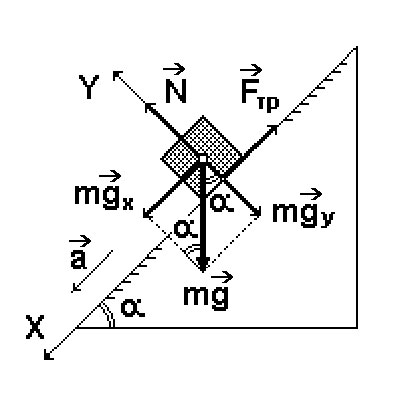
Все силы, действующие на тело, согласно 2-му закону Ньютона, в векторной форме:

$$ m\vec{a} = m\vec{g} + \vec{N} + \vec{F_{тр}} $$

Вес тела на наклонной опоре меньше силы тяжести: $$ N = P = mg cos\alpha $$

Соскальзывание тела с наклонной плоскости происходит, если a > 0, т.е если коэффициент трения скольжения μ < tgα: $$ ma = mg\cdot sin\alpha - F_{тр.скольж} $$ Подставляя в это равенство значение силы трения скольжения \(F_{тр.скольж} = μ \cdot mg\cdot cos\alpha\), получим значение ускорения тела: $$ a = g(sin\alpha - μ\cdot cos\alpha) $$

Если μ > tgα, то тело покоится на наклонной плоскости.

Работа, совершаемая при при подъеме тела по наклонной плоскости

Наклонная плоскость даёт выигрыш в силе, а в работе, наоборот, проигрываем, так как приходится преодолевать силу трения.

Для равномерного движения необходимо, чтобы сумма сил, действующих на тело была рана 0 или сила тяги $$ F_т=F+F_{тр}; \\ F=mg\cdot sin\alpha; \\ F_{тр}=μ\cdot N $$ где N - сила нормального давления, μ - коэффициент трения.

$$ F_{тр} = μ\cdot mg\cdot cos\alpha; \\ F_т=mg\cdot sin\alpha + μ\cdot mg\cdot cos\alpha = mg\cdot(sin\alpha + μ\cdot cos\alpha) $$

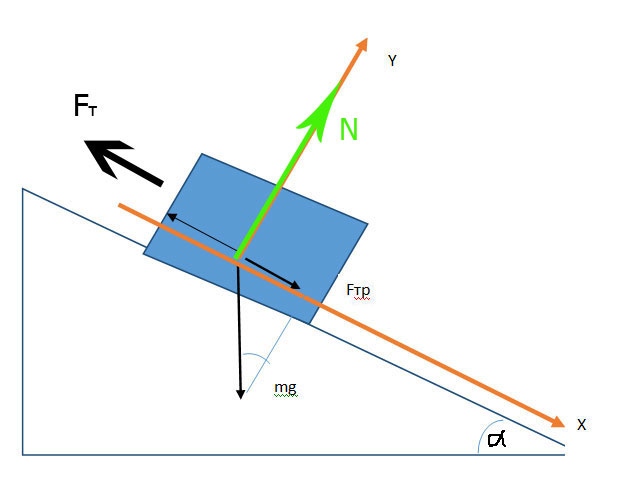
а т.к. \( sin\alpha + μ\cdot cos\alpha \lt 0 \), то \(F_т \lt mg\)

$$ A_п = mgh $$ - работа по подъему тела массой m на высоту h (если поднимаем вертикально);

$$ A_c = F_т\cdot S = mg\cdot(sin\alpha + μ\cdot cos\alpha)\cdot S = mg\cdot(sin\alpha + μ\cdot cos\alpha)\cdot\frac{h}{sin\alpha} $$ - тянем тело по наклонной плоскости высотой h и длиной S, с углом наклона α
Учитываем, что \(S=\frac{h}{sin\alpha}\)

Тогда работа, совершенная при втаскивании тела на высоту h по наклонной: $$ A_c=mgh(1+μ\cdot ctg\alpha)$$ Получаем, что \( A_c \gt A_п\), а значит и КПД наклонной плоскости меньше 1 (из-за трения).

В отсутствие трения КПД наклонной плоскости 1