Что называют рычагом и где применяют рычаги?
Один из самых простых и распространенных механизмов, который изучают в физике еще в 7 классе – рычаг. Рычаг — простейшее механическое устройство, представляющее собой твёрдое тело (перекладину), вращающееся вокруг точки опоры.
Рычагом в физике называют твердое тело, способное вращаться вокруг неподвижной опоры.
Стороны перекладины по бокам от точки опоры называются плечами рычага.
Рычаг используется для получения большего усилия на коротком плече с помощью меньшего усилия на длинном плече (или для получения большего перемещения на длинном плече с помощью меньшего перемещения на коротком плече). Сделав плечо рычага достаточно длинным, теоретически, можно развить любое усилие.
Сущность эффекта рычага заключается в изменении действующей силы по величине и направлению путем передачи через твердое тело места ее приложения. Эффект проявляется на телах различной геометрической формы.
Человек стал использовать рычаг ещё в доисторические времена, интуитивно понимая его принцип. Уже в V тысячелетии до н.э. в Месопотамии использовали принцип рычага для создания равновесных весов. Этот принцип был использован древними римлянами для создания другого измерительного прибора - безмена. В отличие от равновесных весов, плечи безмена были разной длины, причем одно из них могло удлиняться. Чем более тяжелый груз нужно было взвесить, тем длиннее делали раздвижное плечо, на которое подвешивалась гиря. Возведение египетских пирамид не единственный случай применения рычаговых механизмов в древности.
Рычаг использовался повсеместно, но лишь в III в. до н.э. Архимед произвел математические расчеты и создал первую теорию рычага. Поэтому смело можно сказать, что рычаг, опираясь на смекалку древнего человека, взявшего палку и сдвинувшего с ее помощью тяжелый камень, действительно перевернул Землю и предопределил развитие механики.
Разновидности рычагов
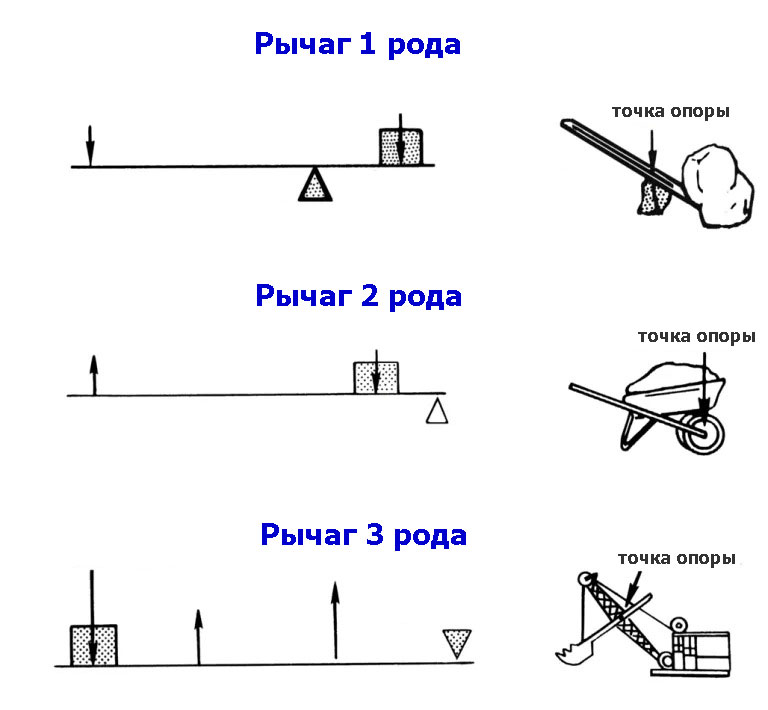
Рычаги делятся на 3 рода, в зависимости от того, куда прикладывается сила, где находится точка опоры и где располагается груз.
- Рычаг 1 рода — это рычаги в которых точка опоры располагается между точками приложения сил.
- Рычаг 2 рода-это рычаги, в которых точки приложения сил располагаются по одну сторону от опоры.
- Рычаги третьего рода — это рычаги, с точкой приложения входящей силы ближе к точке опоры, чем нагрузки, что дает выигрыш в скорости и пути.
Рычаг в быту
Рычаги широко распространены в быту. Вам было бы гораздо сложнее открыть туго завинченный водопроводный кран, если бы у него не было ручки в 3-5 см, которая представляет собой маленький, но очень эффективный рычаг.
То же самое относится к гаечному ключу, которым вы откручиваете или закручиваете болт или гайку. Чем длиннее ключ, тем легче вам будет открутить эту гайку, или наоборот, тем туже вы сможете её затянуть.
При работе с особо крупными и тяжелыми болтами и гайками, например при ремонте различных механизмов, автомобилей, станков, используют гаечные ключи с рукояткой до метра.
Другой яркий пример рычага в повседневной жизни - самая обычная дверь. Попробуйте открыть дверь, толкая её возле крепления петель. Дверь будет поддаваться очень тяжело. Но чем дальше от дверных петель будет располагаться точка приложения усилия, тем легче вам будет открыть дверь.
Рычаги в технике
Механизмы, в которых используется рычаг
Ножницы. Плоскогубцы, качели (перекладина на опоре), тачка (точка опоры - колесо), задняя дверь или капот легкового автомобиля, лом как средство приподнимания тяжелых предметов, руки и ноги человека или животного, ворот колодца с ручкой, отвертка, педали велосипеда, рулевое колесо автомобиля, подъемник с лебедкой, башенный кран.
Интересные факты о рычаге
Автомашину массой в несколько тонн шофер легко приподнимает при помощи домкрата. Домкрат - это тот же рычаг, который дает выигрыш в силе примерно в 40-50 раз.
Ножницы, плоскогубцы, клещи, кусачки и многие другие инструменты - все это рычаги. Сдвигая колечки ножниц или ручки кусачек, взрослый человек действует обычно с силой в 40-50 H. Так как одно плечо может превысить другое раз в 20, то оказывается, что мы способны "вгрызаться в металл" с силой в 1000 H. И это при помощи столь несложного инструмента!
Утверждают, что великий ученый Архимед как-то писал сиракузскому царю Гиерону: "Если бы была другая Земля, я перешел бы на нее и сдвинул бы нашу Землю".
Что такое равновесие рычага?
Физическая величина, равная произведению силы на плечо называется моментом силы. Рычаг находится в равновесии только тогда, когда момент силы (или сумма моментов, если их несколько), вращающий рычаг против часовой стрелки численно равен сумме моментов сил, вращающих его по часовой стрелке.
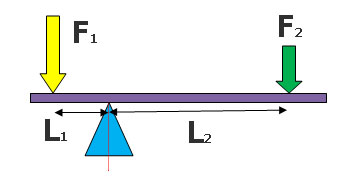
Другими словами, правило равновесия рычага заключается в законе сохранения моментов сил. Таким образом, чтобы работал закон сохранения моментов сил, нужно иметь минимум две силы, у каждой из этих сил будет собственное плечо (расстояние от положения равновесия). Отсюда правило рычага: $$ M_1 = M_2 \\ M_1 = F_1L_1 \;\;\;\; M_2 = F_2L_2 $$ где \(L_1\) и \(L_2\) - плечи сил. Из этого выражения мы можем посчитать, например, значение первой силы, действующей на рычаг, второй, или какое-либо плечо, зная другие величины.
Следствие: если силы равны, то они расположены на одинаковом расстоянии и по разные стороны от положения равновесия.
Правило равновесия рычага:
Рычаг находится в равновесии, если произведение силы на плечо левого рычага равно произведению силы на плечо правого рычага. При этом силы, приложенные к рычагам должны быть направленны соответственно по часовой и против часовой стрелки: $$ \boxed{\frac{F_2}{F_1}=\frac{L_1}{L_2}} $$Или: рычаг находится в равновесии тогда, когда силы, действующие на него, обратно пропорциональны плечам этих сил
Золотое правило механики
Ни один из простых механизмов не даёт выигрыша в работе. Во сколько раз выигрываем в силе, во столько же раз проигрываем в расстоянии, и наоборот.
Золотое правило механики есть не что иное, как простой вариант закона сохранения энергии. Запишем: $$ A_1 = A_2 \\ F_1\cdot L_1 = F_2\cdot L_2 $$ здесь F - сила, L - плечо. Или: $$ \frac{F_2}{F_1} = \frac{L_1}{L_2} $$ т.е. во сколько раз мы выигрываем в силе, во столько же раз нам приходиться проигрывать в расстоянии
Чем отличаются друг от друга рычаги первого и второго рода?
В рычагах первого рода точка опоры располагается между точками приложения сил (детские качели (перекладина), ножницы).
В рычагах второго рода точки приложения сил располагаются по одну сторону от опоры: тачка (точка опоры — колесо), приподнимание предмета ломом движением вверх.
Выполняется ли "золотое правило механики" для рычага?
Как раз это основное применение данного правила - за счет бОльшего рычага и мЕньшей силы мы можем уравновесить бОльшую силу с мЕньшим рычагом.
Например, катаясь на качелях (перекладина), маленький мальчик может "перевесить" взрослого, если взрослый сядет ближе к точке опоры качели.
Приведите примеры рычагов в живой природе. Дают ли эти рычаги выигрыш в силе или перемещении?
Тело человека как рычаг. К примеру, скелет и опорно-двигательная система человека или любого животного состоит из десятков и сотен рычагов. Взглянем на локтевой сустав. Лучевая и плечевая кости соединятся вместе хрящом, к ним также присоединяются мышцы бицепса и трицепса. Вот мы и получаем простейший механизм рычага. В данном случае предплечье дает выигрыш в перемещении.
Какие рычаги используются в технике?
Самый очевидный пример рычаг переключения коробки передач в автомобиле. Короткое плечо рычага та его часть, что вы видите в салоне.
Длинное плечо рычага скрыто под днищем автомобиля, и длиннее короткого примерно в два раза. Когда вы переставляете рычаг из одного положения в другое, длинное плечо в коробке передач переключает соответствующие механизмы.
Здесь так же очень наглядно можно увидеть, как длина плеча рычага, диапазон его хода и сила, необходимая для его сдвига, соотносятся друг с другом.
Например, в спортивных автомобилях, для более быстрого переключения передач, рычаг обычно устанавливают короткий, и диапазон его хода так же делают коротким.
Однако, в этом случае водителю необходимо прилагать больше усилий, чтобы переключить передачу. Напротив, в большегрузных автомобилях, где механизмы сами по себе тяжелее, рычаг делают длиннее, и диапазон его хода так же длиннее, чем в легковом автомобиле.
Встречаются ли рычаги у растений?
Тычинки цветка шалфея представляют собой своеобразные рычаги. От оси тычинок отходят два плеча: длинное и короткое. На конце длинного изогнутого, как коромысло плеча, висит пыльцевой мешочек, а короткое плечо сплющено. Оно закрывает вход в глубину цветка, где находится нектар. Шмель, пытаясь дотянуться до нектара, обязательно задевает короткое плечо. При этом длинное плечо опускается, осыпая спинку шмеля пыльцой. А шмель летит дальше, касается рыльца пестика нового цветка и опыляет его.
Определите рычагом какого рода являются: ножницы, гаечный ключ, лопата
Рычаги 3-го рода выделяют из группы рычагов 2-го рода. Ножницы - рычаг 1-го рода, гаечный ключ — рычаг 2-го рода, а лопата — рычаг 3-го рода
