При горизонтальном броске с начальной скоростью \(v_0\) движение тела удобно рассматривать как два движения: равномерное вдоль оси ОХ (вдоль оси ОХ нет никаких сил препятствующих или помогающих движению) и равноускоренное движение вдоль оси OY.
Скорость в любой момент времени направлена по касательной к траектории. Ее можно разложить на две составляющие: горизонтальную и вертикальную. Горизонтальная составляющая всегда остается неизменной и равна \(v_x = v_0\)
Тело, брошенное горизонтально, движется по параболе. Скорость тела в любой момент времени направлена по касательной к параболе.Модуль скорости можно рассчитать по теореме Пифагора:
$$ ~\upsilon = \sqrt{\upsilon^2_x + \upsilon^2_y} = \sqrt{\upsilon^2_0 + (gt)^2}$$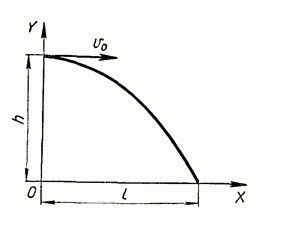
Время падения тела на землю никак не зависит от того, с какой горизонтальной скоростью его бросили, а определяется только высотой, с которой было брошено тело
Основные формулы для решения задач, когда тело брошено горизонтально:
| Время падения | \(t_{пад}=\sqrt{\frac{2h_0}{g}}\), где \(h_0\) - высота, с которой бросили тело |
| Дальность полета | \(L=v_0t_{пад}=v_0\sqrt{\frac{2h_0}{g}}\) |
| Модуль мгновенной скорости в момент времени t | \(v=\sqrt{v_0^2 + (gt)^2}\) |
| Мгновенная высота в выбранный момент времени t (вычисляется по формуле координаты y) | \(y=y_0 + v_{0_y}t + \frac{g_yt^2}{2} = h_0 - \frac{g_yt^2}{2}\), где \(h_0\) - высота, с которой бросили тело |