Тело массой = 0,5 кг падает свободно с высоты 10 метров. На высоте 5 метров в тело попадает и застревает в нём пуля массой = 10 грамм, летевшая горизонтально со скоростью 500 м/с. Найти величину скорости тела и угол, который образует вектор скорости с горизонтом в момент после удара.

По ЗСИ mV1+MV2=(m+M)V
откуда V= (mV1+MV2)/(m+M) 
скорость тела массой M=0,5 кг нам неизвестна
Однако мы знаем высоту падения и столкновения
отсюда можно узнать время h=gt^2/2, тогда t=корень из (2h/g)
или корень из 2*5/10=1 т. Е 1 секунда.  Тогда узнаём скорость из формулы V=V0+at
V0=0 a=g, тогда V=gt=10*1=10м/c 
Теперь считаем (0,01*500 + 10*0,5)/(0,5*0.01)=19,6 м/c т. Е это будет скорость системы после удара.  Теперь ищем угол.
По отдельности импульсы равны по 5  т. К  mV1=5  кг*м/c и   MV2 тоже=5  кг*м/c
Авторы задачи не парились, т. Е угол будет равный как с вертикалью, так и с горизонтом.  А значит равен 45 градусов.

Тело брошено под углом 60 градусов к горизонту с начальной скоростью 21 м/с. На какой высоте вектор скорости будет составлять с горизонтом угол 30 градусов?

Запишем закон сохранения импульса в проекциях на горизонтальную ось (это делать можно, так как нет никаких сторонних сил, дающих проекцию на эту ось. Проще говоря, горизонтальная проекция импульса в полете сохраняется).
В начальный момент времени, \( p(0)=m v_0\cdot \cos (\frac {\pi}{3}); \)
В искомый момент времени, \( p(t)=mv\cdot \cos(\frac{\pi}{6}); \)
Более того, в силу закона сохранения импульса, \( p(0)=p(t) \)
Приравниваем.
\( m v_0\cdot \cos (\frac {\pi}{3})=m v\cdot \cos (\frac {\pi}{6}) \)
Выразим отсюда скорость в искомый момент времени.
\( v(t)=v_0\cdot \frac{\cos (\frac{\pi}{3})}{\cos (\frac{\pi}{6})} \)
А теперь кинематика. В проекциях на вертикальную ось, \( v(t)=v_0-gt \)
Приравняем и найдем время.
\( v_0\cdot \frac{\cos (\frac{\pi}{3})}{\cos (\frac{\pi}{6})}=v_0-gt;\\t=\frac {v_0}{g}\cdot \left(1-\frac{\cos (\frac{\pi}{3})}{\cos (\frac{\pi}{6})}\right) \).
Теперь, снова запишем кинематику в проекциях на вертикальную ось: \( v_0t-\frac{gt^2}{2}=h \).
Подставляя сюда время, находим ответ. (сразу напишу его, потому что подстановка оказывается очень громоздкой, и только под конец почти все численные слагаемые убиваются).
\( \boxed{h=\frac {v_0^2}{3g}}=14,7 \)
Ответ: 14,7 м.

Куб с длиной ребра 1 метр двигается относительно к земному наблюдателю со скоростью 75% от скорости света в вакууме. Вектор скорости направлен перпендикулярно двум противоположным граням куба. Определить объём куба относительно земного наблюдателя.

Перпендикулярные направления сохраняются, параллельные сокращаются, следовательно, объем сокращается в такой же мере, что и длина параллельного направления.
Объем в собственной ск = 1, в лабораторной ск объем равен sqrt(1 - v^2/c^2) = sqrt(3)/2
Линейные размеры куба меняются в направлении движения куба
пусть а- ребро куба относительно СО где куб покоится
V1=a^3 - объем в покое
L=a*√1- (0,75*c)^2/c^2=a*√1-9/16=a*√7/4 длина ребра куба в направлении движения
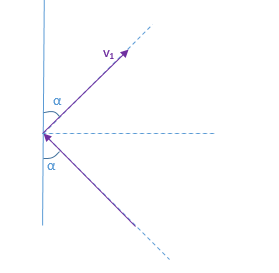
V=a^2*L=a^3*√7/4=0,66143 м3

Теннисный мячик, двигавшийся со скоростью v1, испытывает абсолютно упругое соударение с ракеткой, движущейся ему навстречу со скоростью v2. Вектор скорости мячика в момент удара направлен под углом 45° к плоскости ракетки. Определите величину и направление скорости мячика после отскока от ракетки.

Дано:
v₁
v₂
α=45°
Найти: v, β
Решение:
Если бы ракетка была неподвижна, то мячик отскочил бы под таким же углом и таким же модулем скорости. Этот вектор скорости имеет координаты:
v₁(x)=v₁ cosα=v₁/√2
v₁(y)=v₁ sinα=v₁/√2
v₁(v₁/√2; v₁/√2)
Но ракетка сообщит ему еще одну составляющую v₂. Его координаты
v₂(x)=v₂
v₂(y)=0
v₂(v₂; 0)
Результирующая скорость мяча v является векторной суммой векторов v₁ и v₂. Тогда его координаты:
v(v₂+v₁/√2; v₁/√2)
Из геометрии прямоугольного треугольника имеем
Модуль искомой скорости
v=√((v₂+v₁/√2)²+(v₁/√2)²)=√(v₂²+v₂v₁√2+v₁²)
tgβ=(v₂+v₁/√2)/(v₁/√2)=(v₂√2+v₁)/v₁
β=arctg((v₂√2+v₁)/v₁)
Ответ: v=√(v₂²+v₂v₁√2+v₁²); β=arctg((v₂√2+v₁)/v₁)

Мяч бросили с поверхности Земли под углом 45 градусов со скорость V0= 20 м/с. За какое время вектор скорости мяча повернётся на угол 90 градусов? Сопротивлением воздуха пренебречь. Ускорение свободного падения g=10 м/с^2.

Поскольку угол 45°, то горизонтальная составляющая равна вертикальной и согласно теореме Пифагора равна корню из 20, что составляет 4.47 с. Составим уравнение изменения вертикальной составляющей скорости, учтя направление оси координат вверх V=V0 – a·t или - 4.47 = 4.47 – a·t решив уравнение, получим 0.9 с.