Если тело бросить под углом к горизонту, то в полете на него действуют сила тяжести и сила сопротивления воздуха. Если силой сопротивления пренебречь, то остается единственная сила – сила тяжести. Поэтому, вследствие 2-го закона Ньютона тело движется с ускорением, равным ускорению свободного падения; проекции ускорения на координатные оси равны а х = 0, а у = -g.
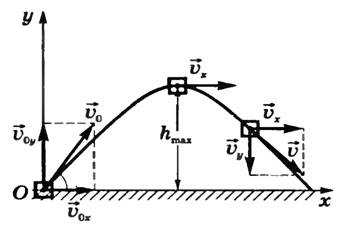
Вектор скорости тела, брошенного под углом к горизонту, направлен по касательной к траектории его движения. Так как начальная скорость направлена не вдоль горизонтальной линии, обе ее проекции отличны от нуля. Проекция начальной скорости на ось ОХ равна v0x = v0cosα. Ее проекция на ось ОУ равна v0y = v0sinα. Проекция мгновенной скорости на ось ОХ равна: vx = v0 cosα. Ее проекция на ось ОУ равна нулю: vy = v0 sinα – gt. Проекция ускорения свободного падения на ось ОХ равна нулю: gx = 0. Ее проекция на ось ОУ равна –g: gy = –g. Отсюда модуль мгновенной скорости в момент времени t можно определить по теореме Пифагора: \(v=\sqrt{v_x^2 + v_y^2}\)
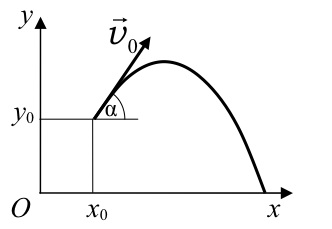
Пусть тело брошено под углом α к горизонту со скоростью \(~\vec \upsilon_0\). Как и в предыдущих случаях, будем пренебрегать сопротивлением воздуха. Для описания движения необходимо выбрать две оси координат — Ox и Oy (рис. 1). Начало отсчета совместим с начальным положением тела. Проекции начальной скорости на оси Oy и Ox\(~\upsilon_{0y} = \upsilon_0 \sin \alpha; \ \upsilon_{0x} = \upsilon_0 \cos \alpha\). Проекции ускорения: gx = 0; gy = -g.
Тогда движение тела будет описываться уравнениями:
Из этих формул следует, что в горизонтальном направлении тело движется равномерно со скоростью \(~\upsilon_x = \upsilon_0 \cos \alpha\), а в вертикальном — равноускоренно.
Траекторией движения тела будет парабола. Учитывая, что в верхней точке параболы υy = 0, можно найти время t1 подъема тела до верхней точки параболы:
Подставив значение t1 в уравнение (3), найдем максимальную высоту подъема тела:
Время полета тела находим из условия, что при t = t2 координата y2 = 0. Следовательно, \(~\upsilon_0 \sin \alpha t_2 - \frac{gt^2_2}{2} = 0\). Отсюда, \(~t_1 = \frac{2 \upsilon_0 \sin \alpha}{g}\) — время полета тела. Сравнивая эту формулу с формулой (5), видим, что t2 = 2 t1. Время движения тела с максимальной высоты t3 = t2 - t1 = 2t1 - t1 = t1. Следовательно, сколько времени тело поднимается на максимальную высоту, столько времени оно опускается с этой высоты. Подставляя в уравнение координаты x (1) значение времени t2, найдем:
Мгновенная скорость в любой точке траектории направлена по касательной к траектории (см. рис. 1). модуль скорости определяется по формуле
Таким образом, движение тела, брошенного под углом к горизонту или в горизонтальном направлении, можно рассматривать как результат двух независимых движений — горизонтального равномерного и вертикального равноускоренного (свободного падения без начальной скорости или движения тела, брошенного вертикально вверх).
На летящее тело кроме силы тяжести ничто не действует.
Вектор скорости имеет вертикальную и горизонтальную составляющие. Тело как бы одновременно участвует в 2-х движениях. Вертикальная составляющая скорости уменьшается с ускорением g=9,8м/с^2 до остановки, потом тело падает с тем же ускорением. А горизонтальному полету ничто не мешает. Трение не учитывается, тело летит по инерции. Так легче подсчитать время полета и высоту, а зная время - дальность.
Поэтому движение вверх - равнозамедленное, потом падение - равноускоренное. По горизонтали движение равномерное.
Сумма проекций векторов дает вектор скорости, с которой на самом деле летит тело.
Формулы для решения задач:
| Время подъема | \(t_{под}=\frac{V_0 sin\alpha}{g}\) |
| Время падения | \(t_{пад}=t_{под}\) |
| Время полета | \(t_{полн}=2t_{под}\) |
| Максимальная высота подъема | \(H=\frac{V_0^2 sin^2\alpha}{2g}\) |
| Дальность полета | \(L=\frac{V_0^2 sin2\alpha}{g}=V_0 cos\alpha t_{полн}\) |
| При фиксированной начальной скорости максимальная горизонтальная дальность достигается при начальном угле 45° и вычисляется по формуле | \(L_{max}=\frac{V_0^2}{g}\) |
| Минимальная скорость тела, брошенного под углом к горизонту | \(v_{min}=v_0 \cdot cos\alpha\) |
| Модуль мгновенной скорости в момент времени t | \(v=\sqrt{v_x^2 + v_y^2}\) |
| Мгновенная высота в выбранный момент времени t | \(y=V_0 sin\alpha t - \frac{gt^2}{2}\) |
| Мгновенная высота в выбранный момент времени t, если тело бросили с высоты \(h_0\) | \(y=h_0 + V_0 sin\alpha t - \frac{gt^2}{2}\) |
Можно ли движение тела, брошенного под углом к горизонту, считать равноускоренным?
Нет. Равнозамедленным - да.
Причина проста: когда ты бросаешь тело с "Земли", то его потенциальная энергия равна, а кинетическая находится на максимальном значении, т.е.
$$ E_k = \frac{mV^2}{2} $$
Получается, что чем большая скорость будет придана телу, тем большее расстояние оно пролетит...
Но главное в том, что ускорение тела будет постоянно замедляться, а затем, в верхней точке, оно будет равно нулю, а далее будет только ускорение свободного падения.
Что происходит с кинетической энергией камня после броска под углом к горизонту?
Кинетическая энергия - \(\frac{mv^2}{2}\) - после старта уменьшается ровно до середины полёта. После этого снова увеличивается до прежнего состояния. Начнет уменьшаться, т.к. с набором высоты будет увеличиваться потенциальная энергия. То есть кинетическая перейдет в потенциальную, а когда тело обратно начнет падать с максимальной высоты, потенциальная энергия начнет переходить в кинетическую. ЗАКОН СОХРАНЕНИЯ МЕХАНИЧЕСКОЙ ЭНЕРГИИ.
В какой точке траектории тела, брошенного под углом к горизонту, его нормальное ускорение будет максимальным? Сопротивлением воздуха пренебречь.
Ускорение тела, брошенного под углом, всегда одинаково и направлено к центру Земли. Во время движения тело меняет направление и ускорение поворачивается относительно тела. Нормальное ускорение - проекция полного ускорения на перпендикуляр к траектории. Это значит что нормальное ускорение будет максимальным тогда, когда полное ускорение будет перпендикулярно траектории. Это происходит в верхней точке траектории тела, брошенного под углом к горизонту. Следовательно, ответ - в верхней точке траектории.