Материальная точка движется по криволинейной траектории. Модуль вектора скорости изменяется со временем по закону υ = (3-2t) м/с. Полное ускорение материальной точки направлено

Из формулы скорости видно, что она уменьшается с течением времени. Скорость направлена по касательной к траектории.
1) ускорение направлено как в случае а, то тело двигалось бы прямолинейно.
2) ускорение направлено как в случае б, то тело двигалось бы криволинейно с увеличением скорости.
3) ускорение направлено как в случае в, то тело двигалось бы по окружности с постоянной скоростью.
4) ускорение направлено как в случае г, то тело двигалось бы криволинейно с уменьшением скорости.
Нам подходит четвертый случай.
Ответ: г

Материальная точка начинает движение в момент времени t=0 и движется вдоль оси ох так что ее координата зависит от времени по закону x=2+6t-1,5t^2. Найдите величину скорости и ускорение точки в момент времени t=3c, а также среднюю путевую скорость за первые дельта t=3с после начала движения

Запишем заданное уравнение в общем виде:
X=Xo+Vo*t+a*t²/2
и в заданном виде:
X = 2 + 6*t - 1,5*t²
Отсюда сразу видно, что Xo=2 м, Vo=6 м/с, а = - 3 м/с².
Скорость - это первая производная от координаты:
V(t) = X’(t) = 6 - 3*t
Тогда в момент t=3 c
V(3)=6-3*3= - 3 м/с   (точка движется в противоположном направлении)
Ускорение - это первая производная от скорости
a (t)  = V ’ (t) = - 3 м/с² (ускорение было найдено нами и выше)
Найдем координату точки через 3 с:
X(3) = 2 + 6*3 - 1,5*3² = 6,5 м
Тогда  средняя путевая скорость:
Vcp = (X-Xo)/t = (6,5-0)/3 ≈ 2,2 м/с

Материальная точка движется по закону x=3t+t найти ускорение скорость и перемещение в момент времени 3с.
Физика, 1 курс.

Х=3t+t². Общий вид уравнения: X=Xo+Voxt+at²/2.
Сопоставляем, видим, что ускорение а=2  м/с²,
начальная скорость Vo=3 м/с.
Уравнение скорости V=3+2t,  V(3)=3+2*3=9 м/с
Перемещение S=3t +t², S(3)=3*3+3²=18м
Скорость v=dx/dt=3+2*t, ускорение a=dv/dt=2, перемещение s=x(3)-x(0). Тогда v(2)=3+2*2=7, a(3)=2, s=x(3)-x(0)=3*3+3²-0=18. 

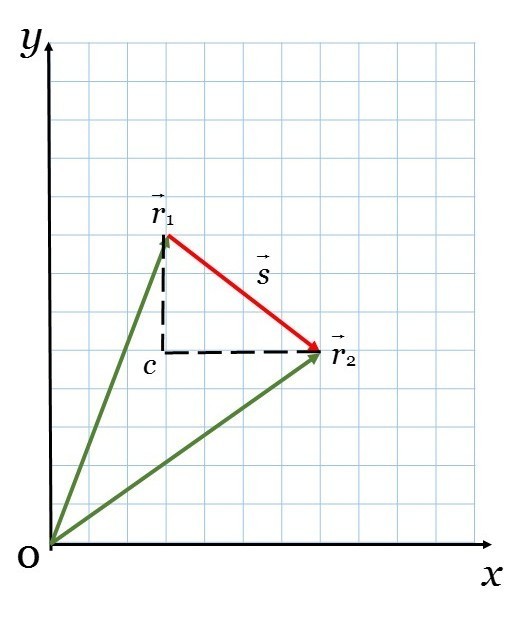
За время t=5c материальная точка A, двигаясь по некоторой, траектории, переместилась из положения с радиус-вектором r1 (3,8) в положение с радиус-вектором r2 (7,5). Найти модуль средней скорости за время t. (Координаты векторов декартовы, в метрах).

Перемещение тела равно разности радиус-векторов его конечного и начального положения. Из чертежа (М: 1кл=1м), рассмотрев прямоугольный треугольник Δr1r2c по теореме Пифагора найдем модуль перемещения
\( s=\sqrt{4^2+3^2}=\sqrt{25}=5 \)
Теперь найдем среднюю скорость. Учитывая что время t=5 с
\( v=\frac{s}{t}=\frac{5}{5}=1 \)(м/с)