Материальная точка массой m=2 кг движется по окружности радиуса R=1 м равномерно со скоростью v=1 v/c. Чему равно и как направлено ускорение точки?
При такой постановке вопроса масса может быть любой, ускорение определяется скоростью (точнее изменением скорости как по модулю так и по направлению. ) При равномерном вращении со скоростью v по окружности радиусом R, ускорение направлено к центру окружности (центростремительное). Его модуль равен:\( a= \frac{v^2}{r} = \frac{1^2}{1}=1 \) м/с²
Маленький груз вертится на натянутой веревке длиной 1 м. В вертикальной плоскости без потери энергии. Центростремительное ускорения груза в самой низкой точке траектории равно 55 м/с. (в квадрате)Чему равно ускорения груза в самой высокой точке траектории (в м/с (в квадрате)? Ускорения свободного падения g=10 м/с. (в квадрате)
Энергия груза в верхней точке mv^2/2+mg*2Rэнергия груза в нижней точке mu^2/2
и они равны
mv^2/2+mg*2R = mu^2/2
a=u^2/R - ускорение в нижней точке
u^2 = a*R
ao=v^2/R - ускорение в верхней точке
ao=v^2/R=(u^2-4gR)/R=a-4g=55-4*10 м/с^2 =50-40 м/с^2 =15 м/с^2 - это ответ
Дано ан=55 м/с2 aв-
ро закону сохранения энергии Eкo=Eп+Eк
m*Vo²/2=m*g*2*R+m*V²/2
Vo²=4*g*R+V²
Vo²/R=4*g+V²/R
Vo²/R=aн
V²/R=aв
ав=ан-4*g=55-40=15 м/с²
При движении велосипедиста по окружности радиусом R с постоянной по модулю скоростью 10м/с его центростремительное ускорение = 5м/с2. С каким центростремительным ускорением будет двигаться велосипедист по окружности радиусом 4R с постоянной по модулю скоростью 20м/с?
Для начала запишем формулу для центростремительного ускорения.a = U² / R
5 = 100/R
R = 20
______
a = 400/20
a = 20
Ответ: 4)20м/с2
а = v²/r следовательно R= v²/a = 100/5 = 20
4R = 80 м
a₂ = v₂²/4R = 400/80 = 5 м/с²
От
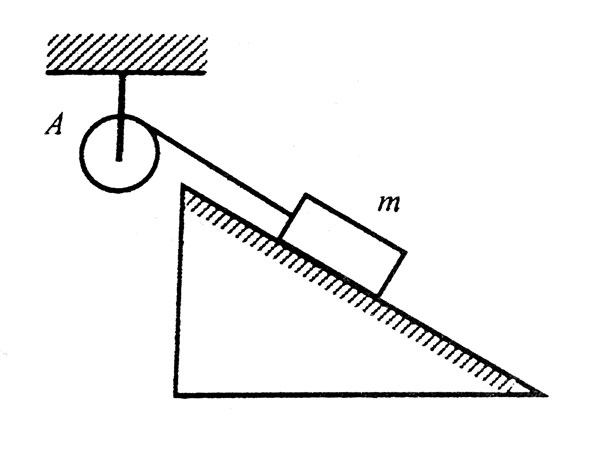
Маховик А приводиться во вращение так, как показано на рис. Момент инерции маховика I, радиус r, масса груза равна m, коэффициент то между грузом и наклонной плоскостью u. Найдите угловое ускорение.
Вычисляешь момент инерции шкива по формуле момента инерции диска:J=m*r²=0,2*0,05²=5*10⁻⁵ кг*м²
Вычисляешь момент инерции маховика по формуле момента инерции кольца:
J=M*R²=1*0,4²=0,16 кг*м²
Суммарный момент инерции всей системы равен
J=0,16+5*10⁻⁵=0,16005 кг*м²
Теперь записываешь второй закон Ньютона для опускающегося груза массой m=0,5 кг в проекции на вертикальную ось:
m*a=m*g-T ❶
T - это сила натяжения нити.
Основное уравнение динамики вращательного движения для системы "маховик+шкив" тоже надо записать:
J*ε=M ❷
Вращающий момент силы натяжения нити равен
M=T*r ❸
Еще надо записать формулу связи между угловым ускорением ε (вращается шкив+маховик) и ускорением груза массой m:
a=ε*r ❹
Откуда она взялась? А все оттуда, из дифференцирования по времени простенькой школьной формулы v=ω*r
Подставляем числа в формулы ❶, ❷, ❸, ❹, получаешь систему линейных уравнений с четырьмя неизвестными. Решаем и находим угловое ускорение ε.
Для вращающегося маховика справедлива формула для угловой скорости
ω=ε*t.