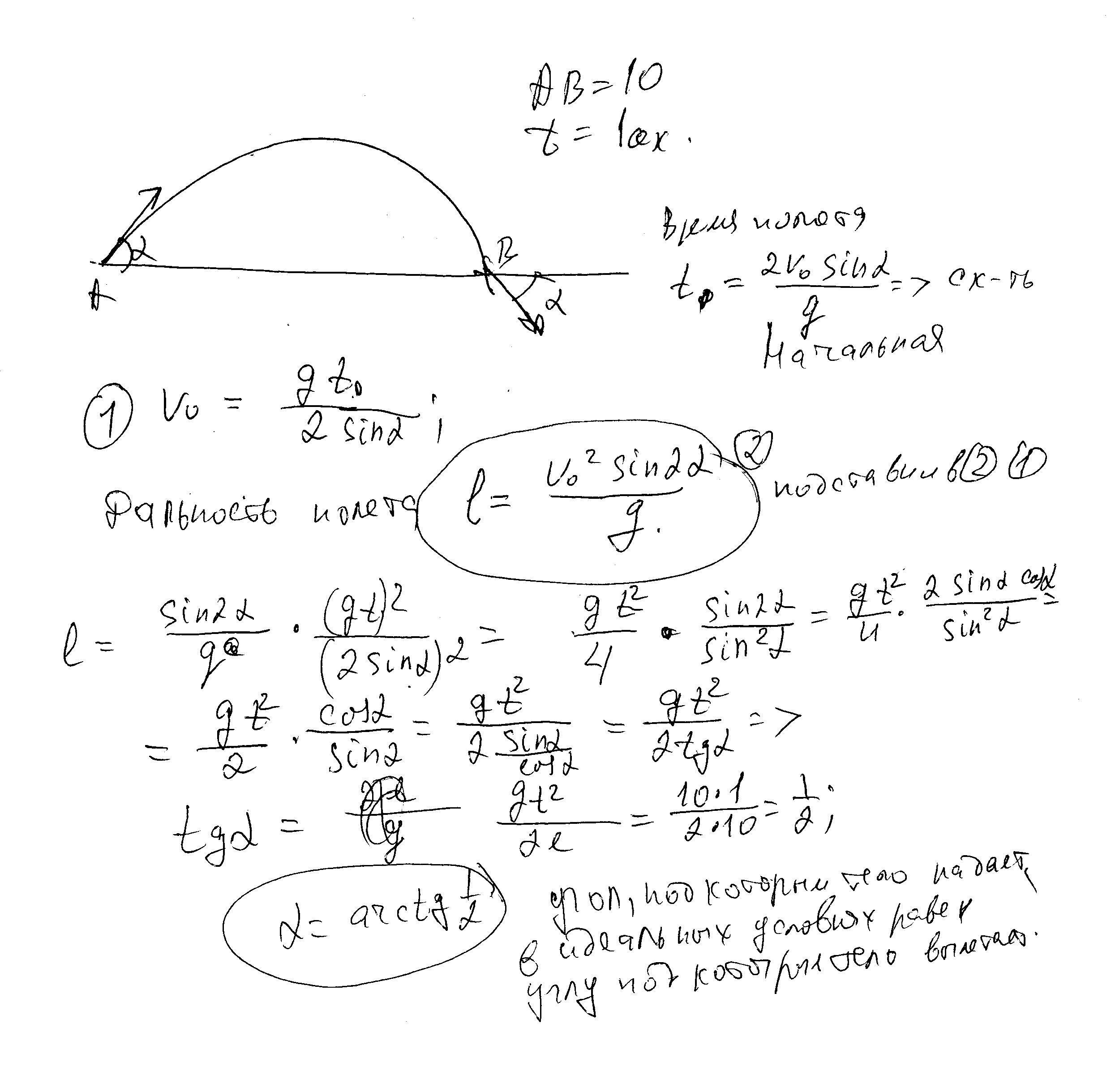
Тело, брошенное горизонтально, приземлилось через 1 с. Если дальность полета 10 м, то под каким углом к горизонту направлена скорость в момент приземления?

Горизонтально тело можно бросить с какой-то высоты, по определению,  тангенс угла падения равен gt/vo
высоту найдем, исходя из того, что начальная скорость по вертикали равна нулю, тогда только горизонтальная проекция определяет дальность полета, vo=l/t=10 м/с, тогда tg a=1 a=45 градусов

На горе с углом наклона к горизонту 30 градусов бросают горизонтально мяч 15 с начальной скоростью 15 м/с. На каком расстоянии от точки бросания вдоль наклонной плоскости он упадет?
В ответе 30 метров, а у меня получается 16. Объясните решение, расстояние в данном случае катет или гипотенуза? Что искать?

Дальность полёта относительно горизонтальной плоскости L=v0*√(2*h/g),
где v0 - начальная скорость тела и h - высота, с которой запущено тело.
В нашем случае L=15*√(2*15/10)=15*√3 м. Но расстояние вдоль наклонной плоскости L1 - это гипотенуза в прямоугольном треугольнике с прилежащим катетом L и углом α=30°. Тогда L1=L/cos(α)=15*√3/(√3/2)=30 м. Ответ: 30 м.

С высокой башни тело брошено горизонтально с начальной скоростью 10 м/с. Через одну секунду из той же точки и с той же по модулю скоростью брошено второе тело. Расстояние между телами через одну секунду после бросания второго тела примерно равно. М.

1) установим начало координат в точке бросания тел
2) определим координаты 1 тела через 2 секунды
x1 = v0*t = 20 м
y1 = - (g t²)/2 = - 20 м
3) определим координаты 2 тела через секунду после броска
x2 = v0*t = 10 м
y2 = - (g t²)/2 = - 5 м
4) вспомним формулу расстояния между двумя точками
d = sqrt(100+225) ≈ 18.03 м

Тело брошено горизонтально со скоростью 10 м/с. Определите скорость тела через 1 с после начала движения, если в этот момент тело еще не достигло земной поверхности

Тело, брошенное горизонтально со скоростью Vx=10м/с движется горизонтально равномерно, если можно не учитывать сопротивление воздуха и одновременно свободно падает с V0=0 и ускорением g.
Vy(t)=V0y+gt, при t=1с Vy(1)=0+9,8*1=10м/с (примерно).
Проекции скорости одинаковые. Чтобы ее найти, надо сложить проекции,
которые являются сторонами квадрата, а скорость его диагональю.  
V^2=Vx^2+Vy^2=100+100=200, V(1)=10√2=14м/с. Через sin45° решено в комментарии. А здесь по т. Пифагора.