На горизонтальной поверхности стола лежит однородный гибкий канат массой M=10 кг. К одному из его концов прикладывают силу F=50 Н, в результате чего он начинает поступательное равномерное движение, оторвавшись от поверхности стола на 40% своей длины. Найдите коэффициент трения скольжения каната о стол. Ответ округлите до десятых. Ускорение свободного падения g=10 м/с2 Считать, что все точки каната находятся в одной вертикальной плоскости.

Приложенная сила F совершила работу против двух сил: тяжести и трения. Работа силы тяжести - это есть потенциальная энергия, приобретённая поднятым куском каната. Итого, стартуем с формулы, на которой будет базироваться всё дальнейшее решение:
А = Еп + Атр
Идём определять компоненты этой формулы.
Потенциальную энергию примем из соображения, что 40% каната поднято так, что центр масс поднятого куска поднялся лишь на половину его длины (типа центр масс находится в центре поднятого куска). Тогда получим такое уравнение:
Еп = 0,4 * М  * g *  1/2 * 0,4 * L
(по ходу, длину каната обозначим буквой L.
Работу силы F примем из соображения, что она действовала на протяжении длины 40% L, следовательно 
А = F * 0,4 * L 
Силы трения будет переменная по мере движения каната, потому что меняется длина остающегося лежать на столе куска каната, следовательно меняется реакция стола N. Примем допущение, что сила трения меняется линейно по мере движения каната. Тогда функция силы трения в зависимости от оставшегося на столе куска каната s выразится так:
Fтр (s) = M * g * mu * s / L
Работа силы трения равна силе трения, умноженной на расстояние.
Атр = Fтр * 0,4 * L
Поскольку функция Fтр линейная (мы приняли такое допущение), то нужно взять среднюю силу трения на участке от начала движения каната до момента окончания движения.
Fтр = (1 + 0,6 ) / 2  * M * g * mu = 0,8 * M * g * mu
Подобьём теперь работу силы трения так:
Атр = 0,8 * M * g * mu * 0,4 * L
Все три компоненты готовы, соберём формулу баланса работы.
Атр = А - Еп
0,8 * M * g * mu * 0,4 * L = F * 0,4 * L - 0,4 * M * g * 1/2 * 0,4 * L
сократим 0,4 * L, останется
0,8 * M * g * mu = F - 0,2 * M * g
отсюда выразим коэффициент трения
mu = (F - 0,2 * M * g ) /  ( 0,8 * M * g )
подставим цифры:
mu = ( 50 - 0,2 * 10 * 10 ) / (  0,8 * 10 * 10 ) = (50-20 ) / 80 = 3/8 =  0,375
округляя до десятых, mu = 0,4

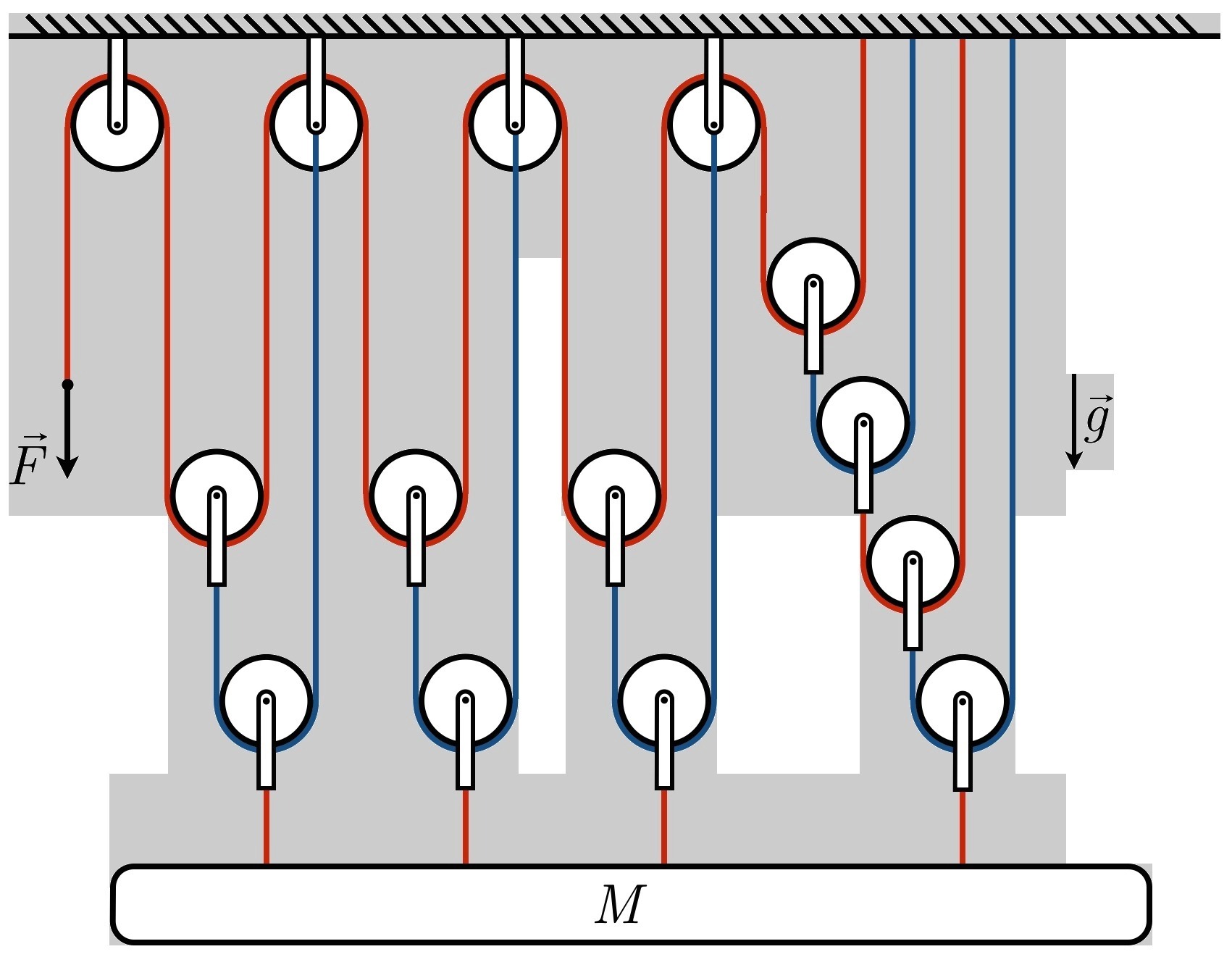
Для удержания очень тяжёлой металлической балки используется система блоков и тросов, прикреплённых к горизонтальной части подъёмного крана, как показано на рисунке. С какой силой F рабочий должен тянуть вниз за конец троса, свисающего с левого блока, чтобы удержать балку массой M=196 кг в равновесии? Ответ выразить в Н, округлив до целых. Точки крепления к ней выбраны таким образом, что она не вращается, а участки тросов, не лежащие на блоках, являются вертикальными. Массой блоков и тросов, а также трением в системе пренебречь. Ускорение свободного падения g=10 Н/кг.

Для трех левых крайних
 3ТКр
Ткр=2Тс  Тс=2Ткрв=2*F
3Ткр=3*2*2*F=12 F
для последнего правого
Ткрпр=2*Тс  Тс=2Ткр1   Ткр1=2Тс2   Тс2=2*F
Ткрпр=16F
в равновесии M*g=12F+16F
F=M*g/28=70 Н ответ

Тело массы m, после свободного падения с некоторой высоты попадает в водоём глубиной L, упруго ударяется о дно и останавливается на половине глубины. С какой высоты H падало тело? Средняя плотность тела равна плотности воды, изменение скорости при ударе о воду и силой сопротивления движению в воздухе пренебречь. Силу сопротивления движению в воде принять в виде F = -k*V, коэффициент k считать известным. (V-скорость)

Мы будем считать тело материальной точкой, чтобы не связываться со сложностями, когда тело проникает в воду и погружено частично (все равно это будет малая поправка к решению)
Итак, сначала очевидное, из закона сохранения энергии мы найдем скорость тела на подлете к воде
\( mv^2/2 = mgH\\ v = \sqrt{2gH} \)
При движении в воде сила Архимеда уравновешивается силой тяжести (это следует из условия, причем дважды следует). Поэтому в воде закон Ньютона (что вверх, что вниз) можно записать в следующей форме
\( m\frac{\Delta v}{\Delta t} = -kv = -k\frac{\Delta S}{\Delta t}\\ m\Delta v = -k\Delta S \)
Это для модуля скорости (он все время уменьшается, а при упругом ударе мгновенно меняется направление, но не модуль)
Итак, мы видим, что просуммировав все дельты, мы получим слева полное изменение скорости, а справа - полное расстояние, пройденное телом в воде (3L/2). Отсюда
\( \displaystyle m(0-v) = -k\frac{3L}{2}\\ v = \frac{3kL}{2m}\\ \sqrt{2gH} = \frac{3kL}{2m}\\\\ H = \frac{9k^2L^2}{8gm^2} \)
P.S. (Для старших девочек и мальчиков) НЕ НАДО РЕШАТЬ ДИФУР В ВОДЕ, И БЕЗ НЕГО ВСЕ ЧТО НУЖНО ДЛЯ РЕШЕНИЯ ЛЕГКО ДОСТАТЬ!

Уравнение движения тела в воде:


\( a = -\frac{k}{m}v \ ; \)


Знак минус отражает противоположность силы сопротивления в воде (и соответствующего ускорения) – направлению движения.


Домножим всё на малое приращение времени:    \( \Delta t \to 0, \)    в течение которого скорость и ускорение можно считать неизменными:


\( a \Delta t = -\frac{k}{m}v\Delta t \ ; \)


\( \Delta v = -\frac{k}{m}\Delta s \ ; \)


Раз любое малое приращение скорости в воде пропорционально соответствующему приращению пути, то и всё изменение скорости пропорционально всему подводному пути. При этом при упругом ударе скорость не меняется по модулю, а меняет лишь направление, при этом направление вектора скорости относительно (!) направления траектории, очевидно, остаётся неизменно сонаправленным. Так что всё движение в воде можно рассматривать, как движение на дистанцию    \( \frac{3}{2} L \ \ : \)


\( v_o - 0 = -\frac{k}{m} ( 0 - \frac{3}{2} L ) \ ; \)


\( v_o = \frac{3k}{2m} L \ ; \)


С другой стороны, с точки зрения кинематики равноускоренного движения в воздухе: изменение квадрата скорости равно удвоенному произведению пути и ускорения:


\( v_o^2 - 0 = 2gH \ ; \)


\( v_o^2 = 2gH = ( \frac{3k}{2m} L )^2 \ ; \)


\( H = \frac{9}{8g} ( \frac{kL}{m} )^2 \ ; \)    это ответ.

Корзина массой 3 кг уравновешена на неподвижном блоке при помощью груза такой же массы. В корзину аккуратно кладут груз массой 0.5 кг, система приходит в движение. С какой силой груз давит на дно корзины? Ускорение свободного падения равно 10 м/с

N = 6g/13 = 4.6 H
N - собственно то, что спрашивали, вес положенного в корзину грузика
А как решать? Подсчитать СИЛУ, действующую на систему, она очевидно равна силе тяжести грузика - Fт=0.5 кг*g
Подсчитать УСКОРЕНИЕ системы грузов - а=Fт/(сумму масс) = 0,5*g/(3+3+0.5)
Подсчитать силу со стороны корзины, тормозящую свободное падение грузика (она по третьему закону равна весу грузика в этой системе) N = Fт - 0.5кг*a

Известно, что масса тела равна 36 кг. Какую силу надо приложить, чтобы удержать это в воде? Ускорение свободного падения считать равным 10 м/с2. Средняя плотность тела равна 2400 кг/м3
. Ответ выразите в единицах СИ и округлите до десятых.

На тело в воде действует две силы: 
Сила Архимеда - Fa=rgV
Сила Тяжести - Fтяж. =mg
1) Fтяж. =36кг*10м/c^2=360Н
Для того чтобы найти объем тела нужно воспользоваться формулой
m=r*V 
из этого следует что V=m/r
V=36кг/2400кг/м3= 0,015м3 
плотность воды =1000 кг/м3
2)Fa= 1000 кг/м3*10м/c2*0.015м3= 150Н
3)Fуд. = Fтяж. Fa= 360Н-150H= 210H