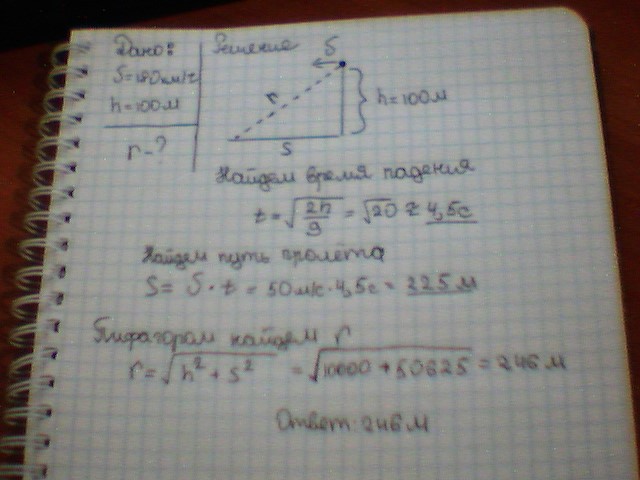С высоты 100 м без начальной скорости падает тело. Найдите путь за последнюю секунду падения.

Направим ось у вниз, тогда g в проекции будет +,
Запишем уравнения координат для равноускоренного движения,
y=yo+Vo+at^2/2 в нашем примере Vo и уо отсутствует, и заменим у на h
получим: h=gt^2/2 умножим все на 2, 2h=gt^2 разделим обе части на "g",
t^2=2h/g, потом все под корень t=Корень из 2h/g=приблизительно 4.5(с)
Последняя секунда-это от 3.50 до 4.50 подставим в уравнение t=3.5
h=gt^2/2=1(0*3.5^2)/2=приблизительно 61, найдем путь за последнюю секунду (т.е. От 3.5 до 4.5) за 4.5 тело прошло 100(м), а за 3.5 прошла 61(м), следовательно, за последнюю секунду 100-61=39(м)
Ответ:39(м)

Чему равно отношение путей, пройденных телом за 4 с и за 5 с после начала свободного падения?

В случае движения без начальной скорости: s2=a*4/2-a*1/2=a*3/2 s3=a*9/2-a*4/2=a*5/2 s3/s2=5/3
a-ускорение s2-расстояние за 2 -ю секунду s3- расстояние за 3-ю секунду a-ускорение свободного падения =9,8м/с^2
H1 = g·t²/2
H2 = g·(t+1)²/2
H2 / H1 = (t+1)² / t²
Если t = 4, то:
H1 / H2 = 4² / 5²  (это закон ОТНОШЕНИЯ путей)
(или, например 16 / 25)

Тело начинает свободное падение с высоты 500 м без начальной скорости. Какую часть пути тело пройдет: 1) за четвертую секунду; 2) за 10 секунду движения?

Пути, проходимые телом при свободном падении за равные промежутки времени относятся как ряд нечетных чисел.
S₁ : S₂ : S₃ :. = 1 : 3 : 5 :.
За первую секунду тело пройдет S₁ = g*t²/2 = 10*1²/2 = 5 м
S₁ / S₄ = 1 / 7 => 5 м / S₄ = 1 / 7 => S4 = 5 м *7 = 35 м
Тело за 4-ю секунду пройдет 35 м
S₁ / S₁₀ = 1 / 19 => S₁₀ = S₁ * 19 = 5 м * 19 = 95 м пройдет за 10-ю секунду
S₄ / S = 35 м / 500 м = 0,07
S₁₀ / S = 95 м / 500 м = 0,19

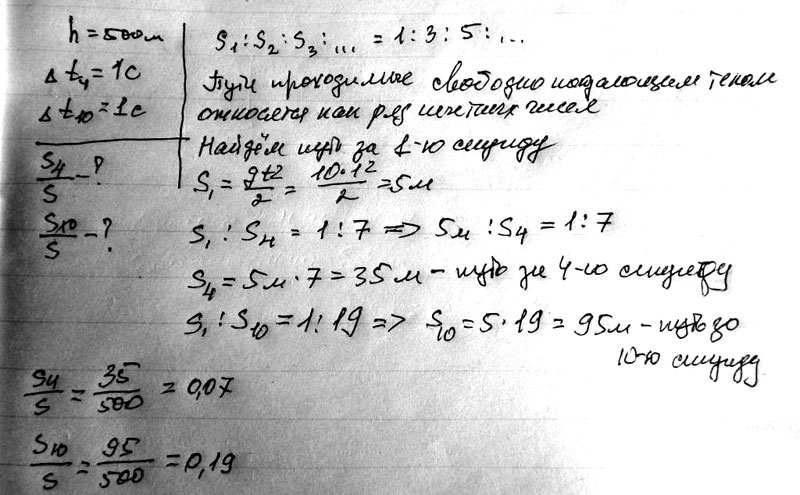
С поверхности земли под углом α=45∘ к горизонту выстрелила пушка. Через время t=38 с она поразила наземную цель. Определите дальность полёта снаряда без учёта сопротивления воздуха. Пушка и её цель расположены на одном горизонтальном уровне. Размеры пушки, её снаряда и цели не учитывать. Ускорение свободного падения g=10 м/с2

Дано: α=45°, t=38c
Найти: l
Решение:
1) V = S ÷ t => S = V × t. Отметим, что дальность полета рассчитывается по оси ОХ, следовательно, скорость нужно брать в проекции на ось ОХ. Тогда формулу можно переписать в виде: l = Vx × t
2) Нам неизвестна начальная скорость. Выразим ее через время полета: Vy = V0y - g(y)×t <=> V0y = g(y)×t => t = V0y ÷ g(y) <=> t (общее) = 2 × V0×sinα ÷ g(y), откуда начальная скорость V0 = t×g(y) ÷ 2×sinα
Тогда в проекции на ось ОХ начальная скорость равна: V0 = ctgα × t × g(y) ÷ 2.
Возвращаясь к основной формуле: l =  ctgα × t × g(y) ÷ 2 × t = ctgα × g(y) × \( t^{2} \) ÷ 2
l = 1 × \( 38^{2} \) × 10 ÷ 2 = 7 220 м

С самолета, летящего со скоростью v = 180 км/ч на высоте H = 100 м, сбрасывают груз. Определить длину вектора перемещения груза до точки падения, а также направление движения груза в момент касания земли.

Груз будет двигаться одновременно вниз с ускорением g и без начальной скорости, и в сторону движения самолета равномерно со скоростью самолета.
Рассчитаем время до падения: 
 = 10с
v = 150 м/с
За это время груз в горизонтальном направлении пролетит l = v*t = 150 * 10 = 150