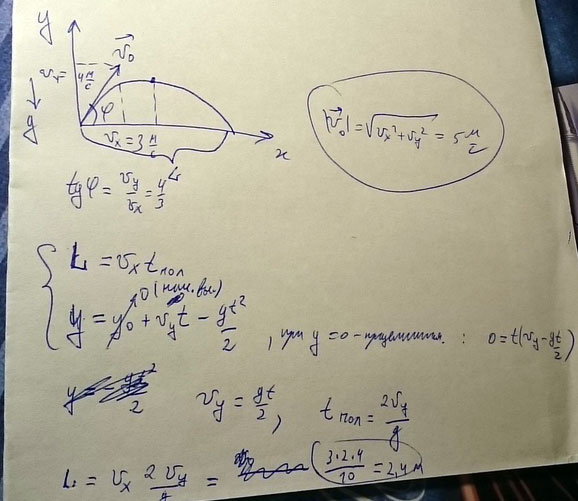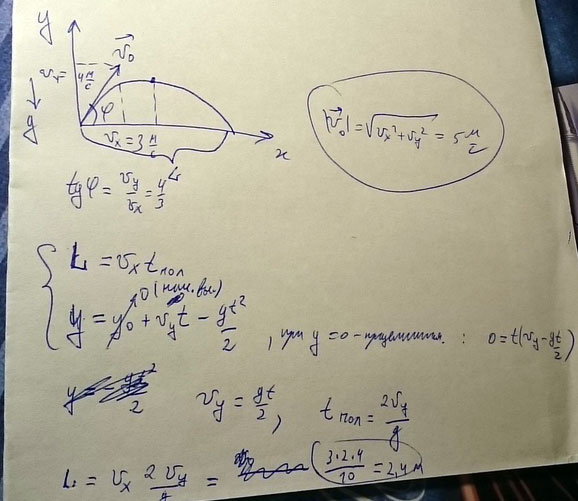Тело массой 2 кг бросили под углом к горизонту с начальной скоростью 12м/с. Пренебрегая сопротивлением воздуха, найти приращение импульса тела за первые 0,5 с движения
,

Δp = m(v1 - v2) = m(dv/dt)Δt = mgΔt Приращение импульса материальной точки за некоторый промежуток времени) при воздействии постоянной силы (в данном случае - силы тяжести) равно произведению величины этой силы на промежуток времени.
Δp = 2*10*0,5 = 10 Ньютонов-секунд
Кстати, поскольку во время свободного полёта сила тяжести постоянна, приращение импульса за первые полсекунды движения равно приращению импульса за любые другие полсекунды всего времени полёта.

Известно, что дальность полета тела, брошенного под углом к горизонту α = 45°, наибольшая. Почему спортсмен толкает ядро под углом меньше 45°?

потому что данное утверждение справедливо если бросок делают с поверхности Земли а у спортсмена есть РОст, значит начальная высота в момент броска не равна нулю по этой причине бросок делают под углом чуть меньше чем 45 градусов. Для каждого роста есть свой угол который даст максимальный результат

Мяч был брошен игроком под углом 45 к горизонту с начальной скоростью 15 м/с. Определите радиус кривизны траектории мяча в точке, когда его скорость составит угол 60 с вертикалью. Ускорение свободного падения считать равным 10 м/с^2

Радиус кривизны траектории свободно летящего тела с мгновенной скоростью v, направленной под углом к вертикали  можно найти из уравнения
g₁ = v²/R где g₁ - проекция ускорения свободного падения на нормаль к вектору мгновенной скорости V
R = V²/g₁
Если вектор мгновенной скорости направлен под углом ф к вертикали, нормальная составляющая g₁ = gSinф = gSin60 = (g√3)/2
Горизонтальная составляющая мгновенной скорости постоянна и для броска под углом 45 градусов равна
Vx = (V₀√2)/2 где V₀ - модуль полной скорости броска.
Модуль мгновенной  скорости под углом 60 градусов к вертикали равен
V = Vx/Sin60 = (2Vx)/√3 = V₀√(2/3)
Таким образом, радиус кривизны траектории мяча, брошенного под углом 45 градусов с начальной скоростью V₀ в момент, когда вектор скорости находится под углом 60 градусов к вертикали равен
R = V₀²(2/3)2/(g√3) = (4/3)V₀²/(g√3) = 225*4/(3*1.73*10) = 17.3 м

Тело массой 100 г, брошенное с земли под углом к горизонту, достигло наибольшей высоты 1,25 м. Найдите модуль вектора изменения импульса за время всего полета тела от броска до падения.

M=0,1 кг
h=1,25 м
g=10 м/с^2
|Δp|=?
Решение.
|Δp|=|mu-mu0|
Что нам неизвестно?
скорость неизвестна.
тело брошено с начальной скоростью
uo=0
поэтому модуль изменения импульса равен :
|Δp|=|mu|
Осталось определить скорость
u=uo-gt
u=-gt(так как uo=0; скорость не пугайся может быть отрицательной это означает, что тело движется замедленно, а у нас так и выходит тело движется вверх и замедляется, а у нас как раз этот случай)
Время полета найдем следующим образом:
1)Тело поднялось на h=1,25 метра спрашивается за сколько!
S=h=uot+gt^2/2
t= √2h/g(движение вверх)= √
2*1,25/10=0,5 секунды
Естественно и двигался обратно он до h=0, тоже 0,5секунды|=>t=1 секунды.
u=-gt=-10*1=-10 м/с.
|Δp|=|0,1*(-10)|=|-1|=1 кг*м/с
Ответ:1

Проекция начальной скорости на горизонтальную и вертикальную оси теннисного мяча, брошенного под углом к горизонту, равны 3 и 4 м/с соответственно. Определите начальную скорость и дальность полёта мяча.

Просто нужно найти длину вектора v по его проекция. V=(Vx^2+Vy ^2)^0.5=5 м/с
1 нужно разложить на вертикальную и горизонтальную составляющие
2 начальная вертикальная 3 4 мс определи высоту и время полета
3 зная время и горизонтальную составляющую определи дальность полета