Охотник целится в мишень, находящуюся на одном и том же с ним уровне и на расстоянии 250м от него. Если пуля вылетает из ружья под углом к горизонту со скоростью 550м/с, то под какой должен быть этот угол для точного попадания в мишень?

H = V0y t - (g t^2) / 2 (уравнение координаты y)
H = ( (l sina t) / (cosa t) ) - (g t^2) / 2 (выразил начальную скорость из формулы для длины полета l) 
H = l tga - (g t^2) / 2
H = l tga - 0,5 g ((2 V0 sina) / g)^2 (выразил время)
H = l tga - ((2 V0^2 sin^2a) / g)
H = l tga - 4 H (выражение в скобках без двойки равно удвоенной высоте)
5 H = l tga
(2,5 V0^2 sin^2a) / g = l tga
l g = 2,5 V0^2 tga (расписал тангенс, сократил синусы, разделил обе части уравнения на косинус)
tga = (l g) / (2,5 V0^2)
tga = (2500)/(2.5*550^(2)) ≈ 0.0033 
по таблице Брадиса этому значению примерно соответствуют градусные меры 0°12’ и 45°6’

С утёса высотой h=50м бросили камень со скоростью v0=10 м/с под углом к горизонту a= 30 градусов. Найти через какое время камень будет на высоте h=20 м над уровнем моря и скорость камня на этой высоте.

Дано
V=10 м/с
α=30
H=10 м
h=20 м
Т- 
Vy=Vsinα=5 м/с
определим высот на которую поднимется тело
h1=5t1²   t1=Vy/10   h1=5*Vy²/100=Vy²/20=25/20=1.25 м t1=0.5 c
уравнение движения имеет вид, при падении с наивысшей точки
h=(H+1.25)-5t2² свободное падение  t2=(h-(H+1.25))/5=2.5 c
И так камень поднимался на максимальную высоту t1=0.5c а затем падал от туда на высоту 20 м t2=2.5 c Всего он находился в движении Т=0,5+2,5=3 с

Камень брошенный под углом к горизонту упал на землю через 4с. Чему равны высота и дальность полёта камня, если известно, что во время движения его максимальная скорость была вдвое больше минимальной? Сопротивлением воздуха пренибречь.

t=4 c    vo=2*vx    h=?   s=?
vx=vo*cosα
cosα=vx/vo=0.5    α=60°
tп=vo*sinα/g   время подъема (tп=t/2=4/2=2 c)
vo=g*tп/sinα=10*2/0.866=23.1 м/с
s=vo²*sin2α/g=23.1²*0.866/10=46.2 м
h=vo²*sin²α/(2*g)=23.1²*0.75/(2*10)=20 м
==============================

T = (2 vy)/g - время полета камня. Значит, вертикальная компонента скорости в начальный момент времени равна vy = (g t)/2 = 20 м/c
H = vy²/(2g) = 20 м - максимальная высота подъема камня
L = (v0² sin2α)/g - максимальная дальность полета камня
из условия задачи vmax = 2 vmin
скорость максимальна в начальный и конечный моменты времени, минимальна в максимальной точке подъема, т.е. :
v0 = 2 v0 cosα
cosα = 1/2. Тогда α = 60°
начальная скорость равна v0 = vy/sinα. Дальность полета:
L = (vy/sinα)² * (sin2α/g) = (20/0.866)^(2)*(0.866/10) ≈ 46.19 м

Тело брошено под углом к горизонту со скоростью 15 м/с. На какой высоте скорость камня уменьшиться в 3 раза?

Мы могли бы просто записать закон сохранения энергии
\( \displaystyle \frac{mv_0^2}{2} = mgh+\frac{m(v_0/3)^2}{2}\\\\ h = \frac{4v_0^2}{9g} = 10 \)
Однако, это возможно только при тех углах броска, при которых максимальная высота подъема камня не меньше найденной
\( \displaystyle H_{\max} = \frac{v_0^2\sin^2\alpha}{2g}\geq\frac{4v_0^2}{9g}\\\\ \sin\alpha\geq\arcsin\left(\frac{2\sqrt{2}}{3}\right)\approx70.52^\circ \)

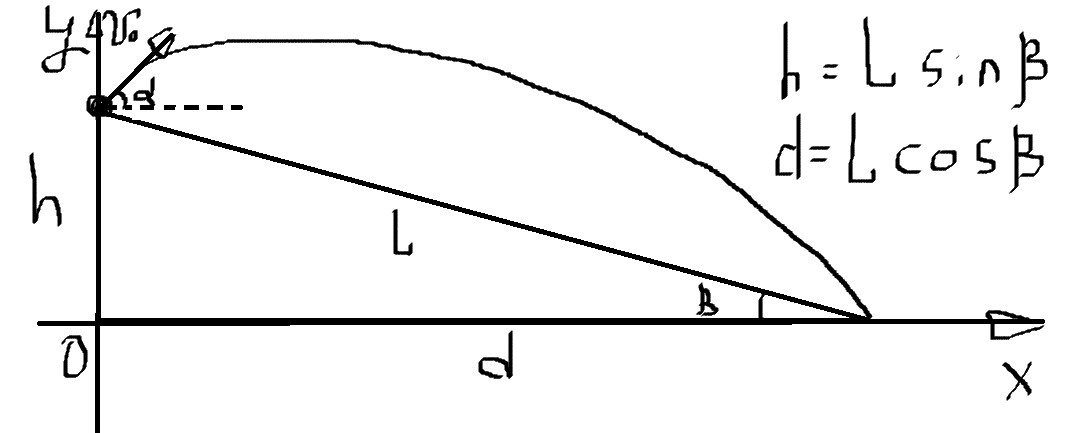
С вершины холма, склон которого составляет с горизонтом угол β=10град, брошен с начальной скоростью v0=15м/с камень вверх под углом α=15град к горизонту. Точка падения камня находится от вершины на расстоянии L (считая вдоль склона холма). Определите L

Идея решения: написать уравнения координат для осей X и Y, выразить перемещения вдоль них через прямоугольный треугольник и решить получившуюся систему уравнений
○ L cosβ = v0 cosα t
○ 0 = L sinβ + v0 sinα t - (g t²)/2
• из первого уравнения t = (L cosβ)/(v0 cosα). Подставляем его во второе:
○ (g/2) * ((L cosβ)/(v0 cosα))² - v0 sinα * (L cosβ)/(v0 cosα) - L sinβ = 0
○ L² * (g cos²β)/(2 v0² cos²α) - L (tgα cosβ + sinβ) = 0
○ L ((g cos²β)/(2 v0² cos²α) L - (tgα cosβ + sinβ)) = 0
○ L = (tgα cosβ + sinβ) * ((2 v0² cos²α)/(g cos²β))
○ L = (0.2679*0.9848+0.1736) * ((2*225*0.933)/(9.8*0.9698)) ≈ 19.3 м