Пуля массой 10 г, летящая горизонтально, ударяется в шар массой 1,1 кг, подвешенный на нити длиной 4,3 м. После абсолютно упругого соударения пуля отскакивает в противоположном направлении, а шар отклоняется от вертикали на 60 градусов. Найти скорость пули после удара. Ускорение свободного падения принять равным 10 м/c2.

Введу обозначения:m_1 - масса пули, m_2 - масса шара, d - длина нити, V_2 - скорость шара после соударения, V_01 - скорость пули до соударения, V_1 - скорость пули после соударения.  
Найдем максимальную высоту подъема шара после соударения.
\( h=d-dcos \alpha =4,3-4,3cos \frac{ \pi }{3}=2,15 \). Затем найдем скорость шара после соударения: согласно закону сохранения энергии \( \frac{m2*V_2^2}{2}=m_2gh \\ V_2= \sqrt{2gh} \). Распишем закон сохранения импульса:\( m_1V_{01}=m_2V_2-m_1V_1 \\ \\ m_2V_2=m_1(V_{01}+V_1) \\ m_2 \sqrt{2gh}= m_1(V_{01}+V_1) \). Теперь закон сохранения энергии системы:\( m_1(V_{01}^2-V_1^2)=m_2*V_2^2 \)(это уравнение уже упрощенное). Дальше составляем систему из двух последних уравнений. Система выглядит во вложении(х - V_01, y-V_1). Решаем ее. x=363,93 y=357,38. Нам нужно y. Поэтому скорость пули после соударения равна 357,38 м/с. Все!

На носу лодки длиной 5 м стоит человек, держа на высоте 1,25 м над лодкой камень массой 4 кг. Человек бросает камень горизонтально вдоль лодки. Какую скорость относительно земли должен сообщить человек камню, чтобы попасть в корму лодки? Масса лодки с человеком равна 246 кг, сопротивление воды и воздуха не учитывайте. Значение ускорения свободного падения примите равным 10 м/с2. Ответ приведите в сантиметрах в секунду

Кинув камень, человек сообщил ему импульс p=m1*v1, при этом сам он получил точно такой же по значению импульс p=m2*v2, но в противоположную сторону.  Раз трения нет, значит надо просто уравнять импульсы камня и лодки. m1*v1=m2*v2. v1=v2*(m2/m1); v1=v2*61,5 То есть скорость камня в 61,5 раза больше скорости лодки Теперь найдём время полёта камня. Его бросили горизонтально, значит падать он будет столько же, как если бы его просто уронили. Время свободного падения тела с высоты h равно t=\( \sqrt{2h/g} \); То есть камень с высоты 1,25м будет падать t=\( \sqrt{2*1.25/10} \)=0,5с
Осталось узнать скорость камня. За время 0,5с он должен преодолеть 5м, значит его скорость будет 5/0,5=10м/с (относительно лодки) Эта скорость состоит (по модулю) из скорости камня относительно земли и скорости лодки относительно земли. Пусть скорость лодки v2, значит общая скорость v2+61.5*v2=10м/с Получаем v2=0,16м/с (скорость лодки) и v1=61,5*v2=9,84м/с. Или в см/с получим 984 см/с. Вроде так как-то

Камень массой 4 кг падает под углом 30 градусов к вертикали со скоростью 10 м/с в тележку с песком общей массой М=16 кг, покоящуюся на горизонтальных рельсах. Определите скорость тележки с камнем после падения в нее камня.

Главное понять, какую проекцию брать: на ось икс или ось игрек. Так как дальнейшее движение будет по иксу, то следовательно лучше взять проекцию на ось икс. И именно закон независимости движения разрешает нам проекцию брать на ось икс и игрек по отдельности.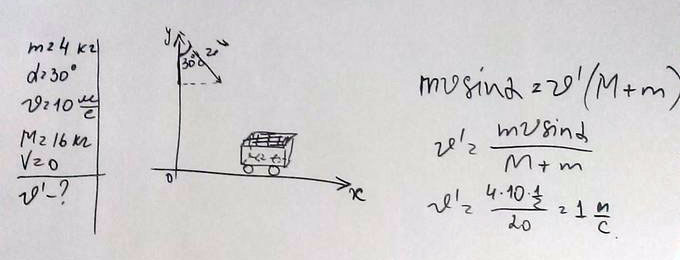

Если из некоторой точки, расположенной на высоте h над землёй, бросить горизонтально со скоростью v0 небольшое тело, то оно упадёт на землю через время t1=1c Если с той же скоростью тело бросить вертикально вверх, то оно упадёт на землю через время t2=2c Определите скорость высоту и дальность полета в 1 опыте ускорения свободного падения = 10 по условию

Найдём V₀ из второго опыта. Тело поднималось вверх 1 секунду (и одну секунду падало).
g=ΔV/Δt ⇒ ΔV = gΔt = 10x1 = 10м/сек.
Определим высоту, с которой брошено тело в первом случае.
H = gt²/2 = 10x1/2 = 5 метров.
Определим дальность полёта.
S = V₀t₁ = 10x1 = 10 м.
Ответ: 10м/сек; 5 м; 10 м.

На шероховатой горизонтальной поверхности стола с коэффициентом трения μ=0,5 находится брусок. Какую скорость V ему нужно сообщить, чтобы через S=150 м его скорость уменьшилась в k=4 раза? Ответ выразить в м/с, округлив до целых. Ускорение свободного падения g=10 м/c2

Дано: u = 0,5   S = 150 м   k = 4   V -
Решение:
1) Решим задачу через работу трения.
С одной стороны, A = - Fтр S = - u mg S.
С другой, A = ΔEk = (m (V/k)^2 / 2) - m V^2 / 2.
Приравняем эти выражения. Получаем:
- u mg S = (V^2 - V^2 k^2) / 2 k^2,
- u mg S = V^2 (1 - k^2) / 2 k^2, откуда выводим V:
V = sqrt(-2 k^2 u g S / (1 - k^2)),
V = sqrt(- 24*10^3 / (1-16)),
V = 40 м/с.