Некая планета имеет такую же массу, как и Земля, но ее радиус в два раза меньше радиуса Земли. Чему равно ускорение свободного падения на поверхности планеты и на высоте 3200км от ее поверхности?
Ускорение свободного падения определяется выражением g = (GM)/R²так как радиус планеты вдвое меньше, то ускорение свободного падения на ней в 4 раза больше, чем на Земле
то есть, g = 4 g(з) = 4*9.8 = 39.2 м/c²
радиус Земли равен R(з) = 6371 км, тогда радиус планеты 6371/2 = 3185.5 км. Во втором случае, на высоте h, расстояние от центра планеты до точки, на которой мы ищем ускорение свободного падения, будет равно: R + h = 3185.5 + 3200 = 6385.5 км
так как величины R(з) и R + h примерно равны, а массы планет одинаковы по условию, то можно утверждать, что ускорение свободного падения на планете на высоте h от ее центра будет приблизительно равно земному, т.е. 9.8 м/c²
Космонавт вступил на недавно открытую планету за пределами Солнечной системы. Масса космонавта вместе с экипировкой составляет 154 кг, а его вес на планете равен 4065,6 Н. Радиус планеты равен 49300 км. Каково будет ускорение свободного падения на планете? Какова масса планеты?
Дано:m=154 кг
P=4065,6 Н
R=49 300 км = 49,3*10⁶ м
______________
g -
M -
Ускорение:
g = P/m = 4065,6/154 ≈ 26,4 м/с²
Из формулы:
g=F/m = G*M*m/(m*R²) = G*M/R²
находим массу планеты:
M = g*R²/G = 26,4*(49,3*10⁶)² / 6,67*10⁻¹¹ ≈ 9,6*10²⁶ кг (почти в 160 раз больше массы Земли и сравнима с массой Сатурна)
1. Определите ускорение свободного падения на поверхности солнца если его радиус равен 6,59 10в пятой степени км масса 2 10в 30степени кг
.Из закона всемирного тяготения F = GmM/Rc^2, при этом F = mg, тогда mg = GmMc/Rc^2. Массу сокращаем, получаем g = GMc/Rc^2. Переводим радиус солнца в метры, это 6,59×10^8. Дальше считаем, g=6.67×10^(-11)×2×10^30/(6,59×10^8)^2≈307м/с^2, при реальном радиусе в 273м/с^2, что можно списать на погрешности при округлении больших чисел. Ответ: g≈307м\с^2
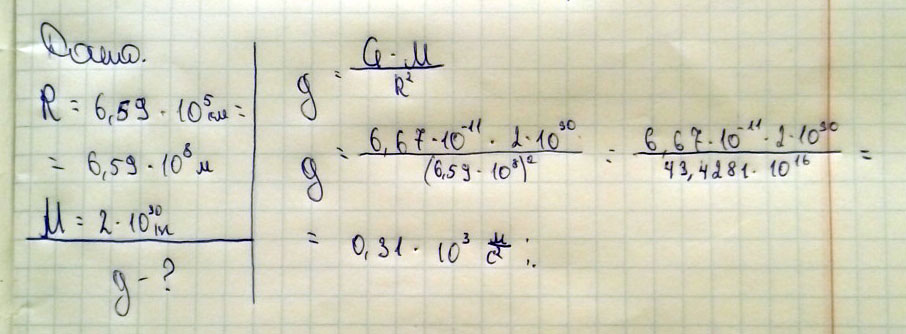
Как вывести ускорение свободного падения (g), но подробно?
Запишем второй закон Ньютона для тела вблизи поверхности Земли\( ma = F_g\\ ma = G\frac{mM}{R^2} \)
Где m - масса тела, M - масса Земли, R - ее радиус. Сократим на m и получим
\( a = \frac{GM}{R^2} \)
Это ускорение одинаково для всех тел, независимо от их массы и это и есть то самое g - ускорение свободного падения
Рассчитать ускорение свободного падения на Меркурии, Венере, Марсе и сравнить с земным.
Формула для ускорения свободного падения находится из 2 закона Ньютона и формулы для силы тяготения\( ma = G\frac{mM}{R^2}\\ a = \frac{GM}{R^2} \)
Мы видим, что ускорение тела вблизи поверхности планеты не зависит от массы тела, а только от радиуса планеты, ее массы и постоянной G=6.67*10^-11
Теперь воспользуемся справочниками
Меркурий
M = 3.3 * 10^23 кг
R = 2240 км
Значит
a = 3.7 м/с^2
Венера
M = 4.9 * 10^24 кг
R = 6050 км
Значит
a = 8.9 м/с^2
Марс
M = 6.4 * 10^23 кг
R = 3400 км
Значит
a = 3.7 м/с^2
Для сравнения на Земле ускорение свободного падения 9.8м/с^2 - это наибольшее среди первых 4 планет Солнечной Системы